Question

You are in a boat traveling perpendicular to waves in water. The wave speed is 8.40 m/s, your speed is 6.50 m/s, and you are heading into the waves. If the wavelength of the waves is 6.70 m, how much time passes between hitting the top of one wave and the next? [This Doppler effect in water is just like that in sound; you can also calculate it from velocities and length.]

_____________ s

Answer 1

Hello and thank you for your question.

First of all let's pick up as much data as we can from the problem:

wave speed is 8.40 m/s then v=8.40 m/s.

From this we can calculate the frequency if we are not moving.

Let's recall the formula to calculate frequency:

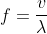
The problem already gives us lambda which is the wavelength, therefore it is 6.70 m

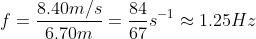
Your speed is vo=6.50 m/s

Now we have enough data to calculate using the Doppler effect equation:

Since we are approaching the waves the frequency of hitting waves will be higher than if we were at full stop, this is the Doppler effect.

Now to answer the problem we simply convert the frequency to a period of time with the formula:

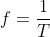
This "T" is the period of time between each wave depending on the frequency.

We are going to use f' which is the frequency of the waves while we move towards them:

This is our final answer.

Hope it helps you!