Question

In matlab:

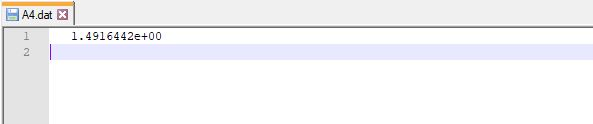
Write a Bisection method with a while-loop that finds the root of the function f(x) = e^(−x) −x^2 + 2 between the values of [−5,5]. Write the function f(x) as a function file (a separate .m file). Use the error tolerance level of “tol = 1e-8.” Save the solved root value in the file A4.dat.

Answer 1

function y = f(x)

y = exp(-x) - x^2 + 2; % compute y = f(x)
  
end

________________________________

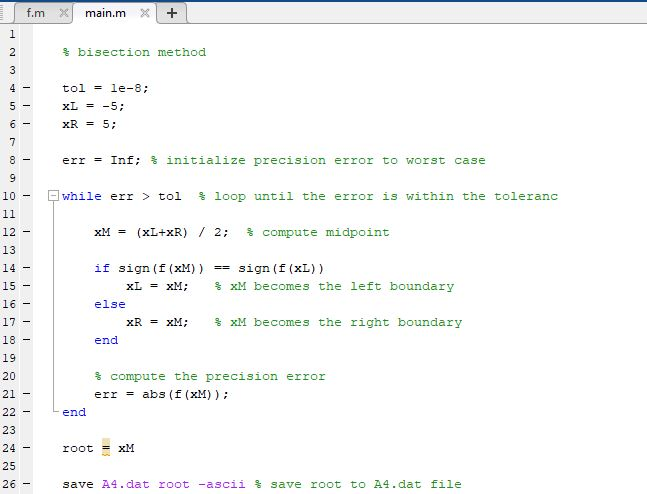
% bisection method

tol = 1e-8;
xL = -5;
xR = 5;

err = Inf; % initialize precision error to worst case

while err > tol % loop until the error is within the toleranc
  
xM = (xL+xR) / 2; % compute midpoint

if sign(f(xM)) == sign(f(xL))
xL = xM; % xM becomes the left boundary
else
xR = xM; % xM becomes the right boundary
end

% compute the precision error
err = abs(f(xM));
end   
  
root = xM

save A4.dat root -ascii % save root to A4.dat file

------------------------------------------------------------------------------
COMMENT DOWN FOR ANY QUERY RELATED TO THIS ANSWER,

IF YOU'RE SATISFIED, GIVE A THUMBS UP
~yc~