Question
In: Physics
Two infinitely long parallel rods carrying uniform charge density lambda are at a distance d from...
Two infinitely long parallel rods carrying uniform charge density lambda are at a distance d from each other. Find the electric force on a particle of charge q* located a distance d directly left of one of the rods. (Derive the formula using Gauss' Law)
Solutions
Expert Solution
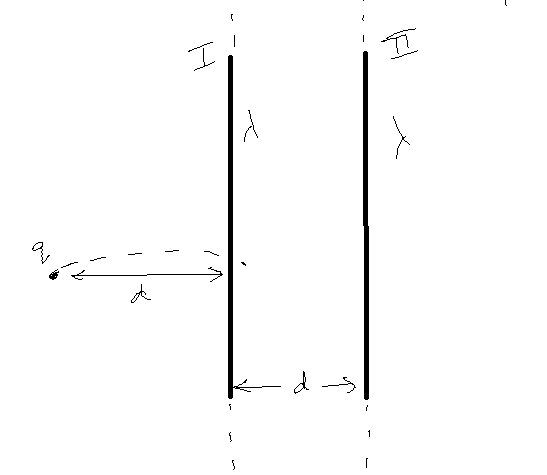
Consider a Gaussian cylindrical surface of radius "d" and length "L" for rod closer to the particle and of radius "2d" and length "L" for rod farther to the particle :
For the closer rod :
A = Area of the Gaussian surface = 2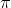 dL
dL
Qenclosed = amount of charge enclosed =  L
L
Ecloser = Electric field by closer rod on the particle
Using Gauss's law
Ecloser A = Qenclosed /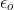
Ecloser (2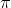 dL) =
dL) =  L/
L/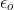
Ecloser = 2 /(4
/(4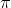
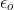 d)
eq-1
d)
eq-1
For the farther rod :
A = Area of the Gaussian surface = 2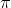 (2d)L
(2d)L
Qenclosed = amount of charge enclosed =  L
L
Efarther = Electric field by farther rod on the particle
Using Gauss's law
Efarther A = Qenclosed /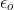
Efarther (4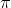 dL) =
dL) =  L/
L/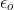
Efarther =  /(4
/(4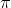
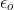 d)
eq-2
d)
eq-2
Using eq-1 and eq-2
E = Total electric field at the location of charge = Ecloser + Efarther
E = 2 /(4
/(4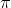
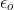 d) +
d) +
 /(4
/(4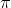
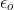 d)
d)
E = 3 /(4
/(4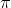
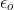 d)
d)
Force on the particle is given as
F = q E
F = 3 q/(4
q/(4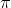
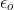 d)
d)
Related Solutions
An infinitely long hollow cylinder of radius R is carrying a uniform surface charge density σ...
3. If you halve the distance from an "infinitely long" line of charge, the magnitude of...
An infinitely long solid cylindrical insulator of radius 13.0 cm has a non-uniform volume charge density...
1.12 [2pt] Consider one infinitely long straight wire with a uniform charge density of 1 C/m....
Consider a long line of charge with linear charge density lambda = 4 micro C/m and...
Two large, flat metal plates are parallel to each other, a distance d apart. A charge...
An infinitely long line of charge has a linear charge density of 5.50×10−12 C/m . A...
An infinitely long line of charge has linear charge density 5.00×10−12 C/m . A proton (mass...
Consider two oppositely charged, isolated parallel plates separated by distance D, with capacitance C, charge Q,...
What is the line charge density on a long wire if a 7.1-μg particle carrying 1.6...
- 1. Explain in detail why it is detrimental to a pediatric patient the use of preservatives...
- Python Write a script to play two-dimensional Tic-Tac-Toe between two human players who alternate entering their...
- IN JAVA PLEASE!! Write a program that initializes an array with ten random integers and then...
- Using the Arizona Wuhan seafood market virus isolate, MN997409.1, run BLAST against the RefSeq Representative genomes...
- ACME manufacturing is a low-cost producer of a single, commodity product: RGL-01. Standard overhead cost information...
- Waterways for Chapter 9 (WCP9sum) Summer Waterways Corporation is preparing its budget for the coming year....
- A bar of length ℓ lies on the ?̂-axis with its center at the origin. A...
 genius_generous answered 2 months ago
genius_generous answered 2 months ago