Let X ∼ Pois(4), Y ∼ Pois(12), U ∼ Pois(3) be independent random variables. a) What...

Let X ∼ Pois(4), Y ∼ Pois(12), U ∼ Pois(3) be independent random variables.

a) What is the exact sampling distribution of W = X + Y + U?
b) Use R to simulate the sampling distribution of W and plot your results. Check that the simulated mean and standard error are close to the theoretical mean and standard error.
c) Use the simulated sampling distribution to estimate P(W ≤ 14) and then check your estimate with an exact calculation.

Expert Solution

please have a look at the R code

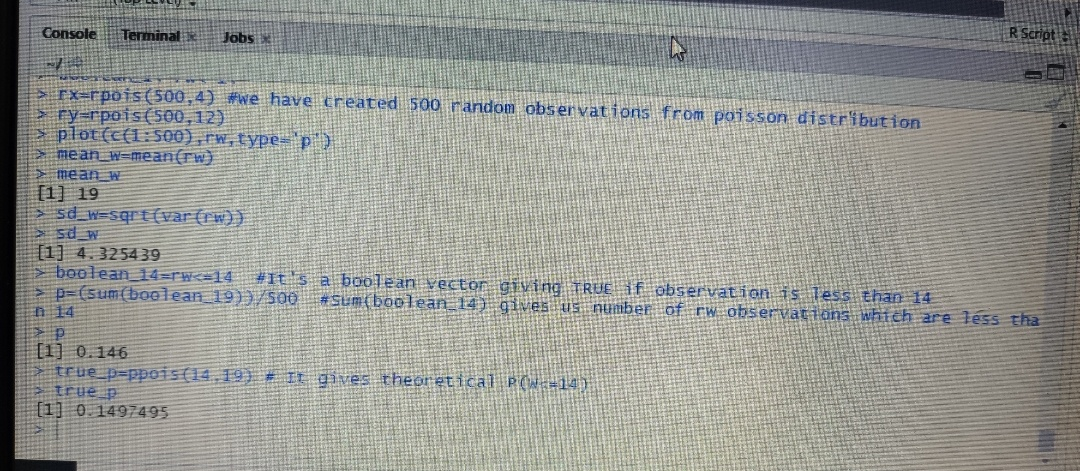
rx=rpois(500,4) #We have created 500 random observations from poisson distribution
ry=rpois(500,12)
ru=rpois(500,3)
rw=rx+ry+ru
plot(c(1:500),rw,type='p')
mean_w=mean(rw)
mean_w
sd_w=sqrt(var(rw))
sd_w
boolean_14=rw<=14 #It's a boolean vector giving TRUE if observation is less than 14
p=(sum(boolean_19))/500 #Sum(boolean_14) gives us number of rw observations which are less than 14
p
true_p=ppois(14,19) # It gives theoretical P(W<=14)
true_p

"Now have a look at the output"

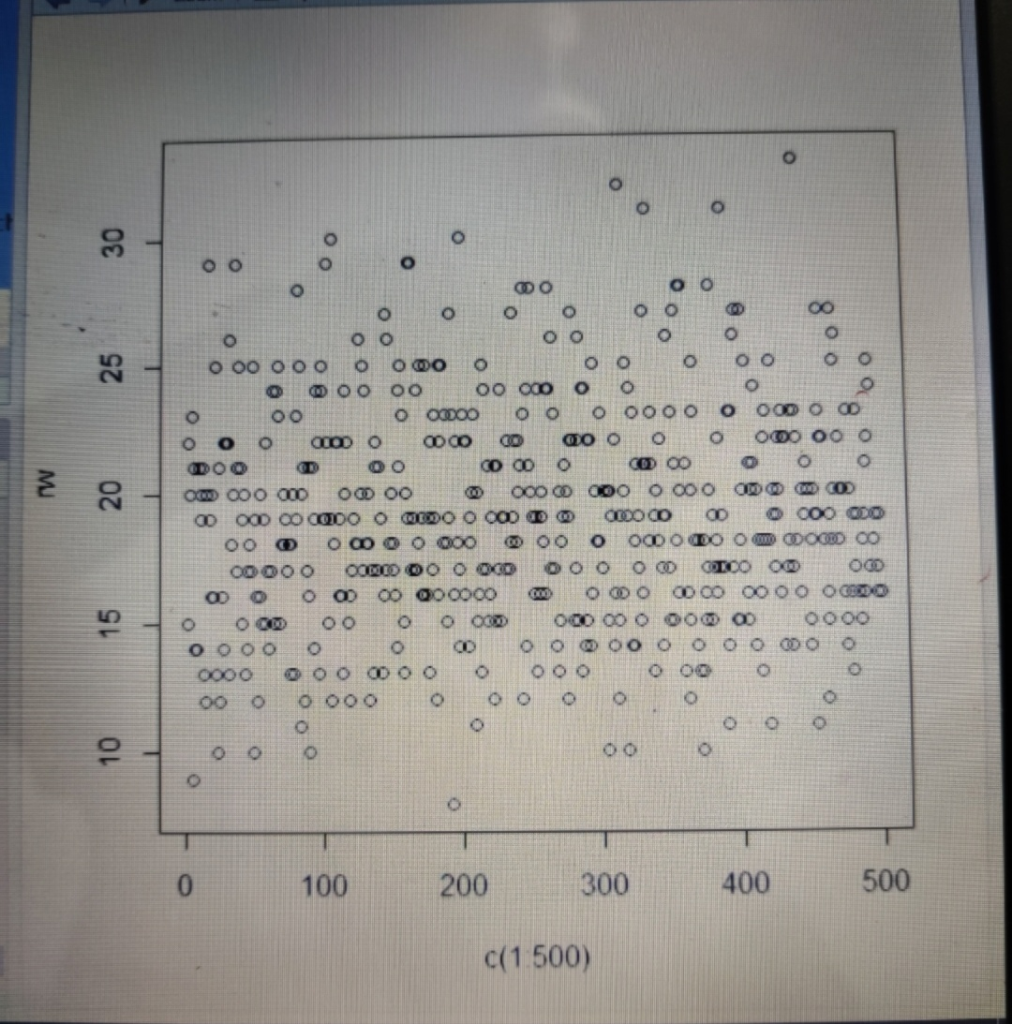
simulated mean is coming out to be theoretical mean and simulated standard devaition (4.325) is very close to actual sd ( root(19)=4.3589). The simulated probabolity (0.146) is very close to actual probability (0.1497)

milcah answered 7 hours ago

1. Let X and Y be independent U[0, 1] random variables, so that the point (X,...

1. Let X and Y be independent U[0, 1] random variables, so that the point (X, Y) is uniformly distributed in the unit square. Let T = X + Y. (a) Find P( 2Y < X ). (b). Find the CDF F(t) of T (for all real numbers t). HINT: For any number t, F(t) = P ( X <= t) is just the area of a part of the unit square. (c). Find the density f(t). REMARK: For a...

Let X and Y be two independent random variables such that X + Y has the...

Let X and Y be two independent random variables such that X + Y has the same density as X. What is Y?

Let X and Y be independent positive random variables. Let Z=X/Y. In what follows, all occurrences...

Let X and Y be independent positive random variables. Let Z=X/Y. In what follows, all occurrences of x, y, z are assumed to be positive numbers. Suppose that X and Y are discrete, with known PMFs, pX and pY. Then, pZ|Y(z|y)=pX(?). What is the argument in the place of the question mark? Suppose that X and Y are continuous, with known PDFs, fX and fY. Provide a formula, analogous to the one in part (a), for fZ|Y(z|y) in terms...

Let X and Y be two independent random variables. X is a binomial (25,0.4) and Y...

Let X and Y be two independent random variables. X is a binomial (25,0.4) and Y is a uniform (0,6). Let W=2X-Y and Z= 2X+Y. a) Find the expected value of X, the expected value of Y, the variance of X and the variance of Y. b) Find the expected value of W. c) Find the variance of W. d) Find the covariance of Z and W. d) Find the covariance of Z and W.

Let X, Y, and Z independent random variables with variance 4 and mean 1. Find the...

Let X, Y, and Z independent random variables with variance 4 and mean 1. Find the correlation coefficient between (X-2YX+1) and (4X+Y)

Let X, Y be independent exponential random variables with mean one. Show that X/(X + Y...

Let X, Y be independent exponential random variables with mean one. Show that X/(X + Y ) is uniformly distributed on [0, 1]. (Please solve it with clear explanations so that I can learn it. I will give thumbs up.)

Let X and Y be independent Gaussian(0,1) random variables. Define the random variables R and Θ,...

Let X and Y be independent Gaussian(0,1) random variables. Define the random variables R and Θ, by R2=X2+Y2,Θ = tan−1(Y/X).You can think of X and Y as the real and the imaginary part of a signal. Similarly, R2 is its power, Θ is the phase, and R is the magnitude of that signal. (b) Find the probability density functions of R and Θ. Are R and Θ independent random variables?

1. Let X and Y be independent random variables with μX= 5, σX= 4, μY= 2,...

1. Let X and Y be independent random variables with μX= 5, σX= 4, μY= 2, and σY= 3. Find the mean and variance of X + Y. Find the mean and variance of X – Y. 2. Porcelain figurines are sold for $10 if flawless, and for $3 if there are minor cosmetic flaws. Of the figurines made by a certain company, 75% are flawless and 25% have minor cosmetic flaws. In a sample of 100 figurines that are...

Let X, Y be independent random variables with X ∼ Uniform([1, 5]) and Y ∼ Uniform([2,...

Let X, Y be independent random variables with X ∼ Uniform([1, 5]) and Y ∼ Uniform([2, 4]). a) FindP(X<Y). b) FindP(X<Y|Y>3) c) FindP(√Y<X<Y).

Let X and Y be two independent random variables, and g : R2 --> R an...

Let X and Y be two independent random variables, and g : R2 --> R an arbitrary bivariate function. 1) Suppose that X and Y are continuous with densities fX and fY . Prove that for any y ? R withfY (y) > 0, the conditional density of the random variable Z = g(X, Y ) given Y = y is the same as the density of the random variable W = g(X, y). 2) Suppose that X and Y...

Question