Question

A 1000-kg car rounds a curve on a flat road of radius 50 m at a speed of 50 km/h (14 m/s). Will the car follow the curve, or will it skid? Assume (a) the pavement is dry and s = 0.60; (b) the pavement is icy and s = 0.25

Answer 1

We will determine the maximum speed that can have the car in each case.

The friction force is given by

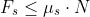
Where:
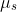  coefficient of static friction.
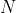  magnitude of normal force

the maximum value of friction force occurs when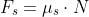

• procedure to find the expression of maximum speed

Newton's second law applies to circulate mimiento

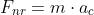
where:
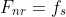net force in radial direction.in this case is only the static friction force which prevents the trolley leaves the court
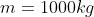mass
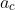  centripetal acceleration

centripetal aceleraion equals where 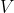is the speed of the car and 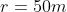the radius

i.e

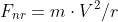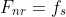but   and

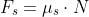
combining equations

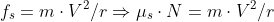
to evaluate the expression of normal add vertical forces.

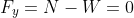
They are:
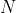  normal up
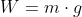  the weight down.
the sum of these forces should be zero, because the car does not accelerate vertically

Now

finally

substituting in the expression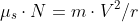

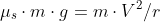
simplifying m.

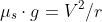
expression for the maximum speed

the expression of the maximum speed

(a) the pavement is dry and s = 0.60

if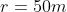

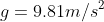
evaluated numerically

the possible maximum speed is higher than the speed at which the car enters the curve.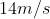

finding: the car follow the curve

(b) the pavement is icy and s = 0.25

if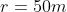

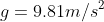
evaluated numerically

the possible maximum speed is less than the speed at which the car enters the curve.

finding: the car will skid.