Question

Skinner's Fish Market buys fresh Boston bluefish daily for $4.2 per kilogram and sells it for $5.7 per kilogram. At the end of each business day, any remaining bluefish is sold to a producer of cat food for $2.4 per kilogram. Daily demand can be approximated by a normal distribution with a mean of 96 kilograms and a standard deviation of 15 kilograms.

What is the optimal stocking level?

*Round your answers to 3 decimal places in your calculation if necessary.

Answer 1

Given

P = Price at which the fish is sold to customers /Kg = $ 5.7

C = Cost at which fish is brought from Boston bluefish / Kg = $ 4.2

S = Salvage value sold to the producer of cat food / Kg = $ 2.4

Demand is approximated by a normal distribution

mean 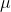= 96

Standard deviation 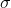= 15

Optimal stocking level = 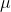+ Z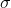

Z = norm.s.inv (Cr)

Cr = critical ratio

Cr = Cu / (Cu +Co)

Cu = cost of underage

Co = cost of overage

Cu = P - C

Cu = $ 5.7 - $ 4.2

Cu = $ 1.5

Co = C - S

Co = $4.2 - $ 2.4

Co = $ 1.8

so Critical ratio (Cr) = 1.5 / ( 1.5 + 1.8)

Cr = 1.5 / 3.3

Cr = 0.4545

We know Z = norm.s.inv(Cr)

Use excel function normsinv to find the value of Z

Z = norm.s.inv (0.4545)

Z = -0.11429

So

Optimal stocking level = 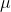+ Z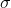

substituting the values

Optimal stocking level = 96 + ( - 0.11429) 15

Optimal stocking level = 96 - 1.7135

Optimal stocking level = 94.28565

Optimal stocking level = 94.286 (Rounding to 3 decimal places)

P.S --Kindly give thumbs up --This will motivate me to provide more and more quality answers!