Question

The determined Wile E. Coyote is out once more to try to capture the elusive roadrunner. The coyote wears a new pair of power roller skates, which provide a constant horizontal acceleration of 15 m/s². The coyote starts off at rest 70 m from the edge of a cliff at the instant the roadrunner zips by in the direction of the cliff.

(a) If the roadrunner moves with constant speed, find the minimum speed the roadrunner must have to reach the cliff before the coyote.

_______ m/s

(b) If the cliff is 100 m above the base of a canyon, find where the coyote lands in the canyon. (Assume that his skates are still in operation when he is in "flight" and that his horizontal component of acceleration remains constant at 15 m/s².)

__________ m from the base

Answer 1

roadrunners A
coyote   B

establishing the position equation for the coyote.

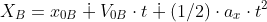
where.
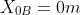Initial position (assuming that starts from the origin)
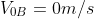initial velocity (part from rest)
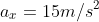acceleration

the time it takes to reach the cliff is calculated

the equation is evaluated when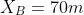

The minimum speed that should have the roadrunner is calculated by the following expression

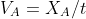
PART B

first we calculate the speed with which the coyote leaves the cliff

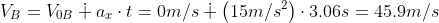
the time it takes to reach the ground is calculated

considerations
the ground as the reference
The positive axes are up and where the coyote moves

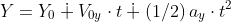
where:
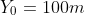  Initial height.
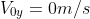initial speed
acceleration of gravity
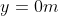when it reaches the ground.

evaluating the equation

The expression for the time

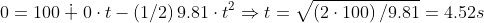
the equation is set for horizontal movement

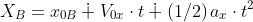
where:
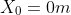From the base of the cliff.
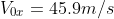Horizontal velocity that starts.
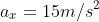   horizontal acceleration
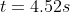     duration of the journey

Evaluating the equation in the given time

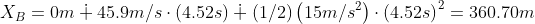
reaches 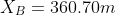from base of the cliff