Question

A box contains 5 fair coins, 4 coins that land heads with probability 1/3 , and 1 coin that lands heads with probability 1/4 . A coin is taken from the box at random and flipped repeatedly until it has landed heads three times. Let X be the number of times that the coin is flipped and Y be the probability that the coin lands heads.

(a) Find the random variables E(X|Y ) and var(X|Y ) in terms of Y .

(b) Compute E(X).

(c) Compute var(X).

Answer 1

Answer:

Let X be the number of times that the coin is flipped and Y be the probability that the coin lands heads.

(a)

The random variable and in terms of Y.

The probability that the coin is flipped times until it has landedheads three times given that the probability that the coin lands heads is .

[Note : note that we have to flip the coin at least 3 times to get heads 3 times so, x can take the values 3,4,5...]

  = The probability that there are 2 heads and trails in the first    flips of the coin and then flip results in head given that the probability that the coin lands heads is

[ The number of ways such that there are 2 heads and tails in flips of the coin is

The probability that the coin lands tails is (2) . here we assume that the tosses are independent ]

  

The conditional pmf of X given Y=y is

  

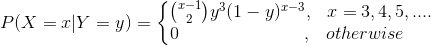
The pmf of X is

Here, NB means Negative Binomial

  

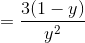
(b)

can be calculated as below:

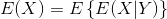
By the law of total expectation

We note that the box contains 5 coins 4 coins that land heads with probability and coins that lands head with probabiliy

  

  

  

(c)

By the law of total variance

  

  

Now,