Question

hpw do a put the program to halt, placing a limit greater than 1 on the eating state for each philosopher in the program below?

#include <pthread.h>

#include <semaphore.h>

#include <stdio.h>

#include <unistd.h>

#define N 5

#define THINKING 2

#define HUNGRY 1

#define EATING 0

#define LEFT (phnum + 4) % N

#define RIGHT (phnum + 1) % N

#define deprecated

int state[N];

int phil[N] = { 0, 1, 2, 3, 4 };

sem_t mutex;

sem_t S[N];

void test(int phnum)

{

if (state[phnum] == HUNGRY

&& state[LEFT] != EATING

&& state[RIGHT] != EATING) {

// state that eating

state[phnum] = EATING;

sleep(2);

printf("Philosopher %d takes fork %d and %d\n",

phnum + 1, LEFT + 1, phnum + 1);

printf("Philosopher %d is Eating\n", phnum + 1);

// sem_post(&S[phnum]) has no effect

// during takefork

// used to wake up hungry philosophers

// during putfork

sem_post(&S[phnum]);

}

}

// take up chopsticks

void take_fork(int phnum)

{

sem_wait(&mutex);

// state that hungry

state[phnum] = HUNGRY;

printf("Philosopher %d is Hungry\n", phnum + 1);

// eat if neighbours are not eating

test(phnum);

sem_post(&mutex);

// if unable to eat wait to be signalled

sem_wait(&S[phnum]);

sleep(1);

}

// put down chopsticks

void put_fork(int phnum)

{

sem_wait(&mutex);

// state that thinking

state[phnum] = THINKING;

printf("Philosopher %d putting fork %d and %d down\n",

phnum + 1, LEFT + 1, phnum + 1);

printf("Philosopher %d is thinking\n", phnum + 1);

if(phnum==N-1){ // this is the last philosopher for which we reverse the order of checking it will first check right then left

test(RIGHT);

test(LEFT);

}

else{ // this is for the remaining philosopher for which the order of checking will be first check left then right

test(LEFT);

test(RIGHT);

}

sem_post(&mutex);

}

void* philospher(void* num)

{

while (1) {

int* i = num;

sleep(1);

take_fork(*i);

sleep(0);

put_fork(*i);

}

}

int main()

{

int i;

pthread_t thread_id[N];

// initialize the semaphores

sem_init(&mutex, 0, 1);

for (i = 0; i < N; i++)

sem_init(&S[i], 0, 0);

for (i = 0; i < N; i++) {

// create philosopher processes

pthread_create(&thread_id[i], NULL,

philospher, &phil[i]);

printf("Philosopher %d is thinking\n", i + 1);

}

for (i = 0; i < N; i++)

pthread_join(thread_id[i], NULL);

}

Answer 1

The Dining Philosophers Problem

The Dining Philosophers problems is a classic synchronization problem (E. W. Dijkstra. Co-operating Sequential Processes. In F. Genuys (ed.) Programming Languages, Academic Press, London, 1965) introducing semaphores as a conceptual synchronization mechanism. The problem is discussed in just about every operating systems textbook.

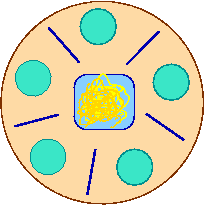Dining Philosophers. There is a dining room containing a circular table with five chairs. At each chair is a plate, and between each plate is a single chopstick. In the middle of the table is a bowl of spaghetti. Near the room are five philosophers who spend most of their time thinking, but who occasionally get hungry and need to eat so they can think some more.

In order to eat, a philosopher must sit at the table, pick up the two chopsticks to the left and right of a plate, then serve and eat the spaghetti on the plate.

Thus, each philosopher is represented by the following pseudocode:

        process P[i]
          while true do
            { THINK;
              PICKUP(CHOPSTICK[i], CHOPSTICK[i+1 mod 5]);
              EAT;
              PUTDOWN(CHOPSTICK[i], CHOPSTICK[i+1 mod 5])
             }

A philosopher may THINK indefinately. Every philosopher who EATs will eventually finish. Philosophers may PICKUP and PUTDOWN their chopsticks in either order, or nondeterministically, but these are atomic actions, and, of course, two philosophers cannot use a single CHOPSTICK at the same time.

The problem is to design a protocol to satisfy the liveness condition: any philosopher who tries to EAT, eventually does.

Discussion. Of course, the best thing is to go off and try to solve this problem on your own by exploring various protocols philosophers might use to acquire chopsticks. You are likely to quickly encounter the same deadlock and livelock scenarios we saw in the mutual exclusion problem, but you will quickly see in this case that mutual exclusion is too primitive a synchronization mechanism for solving this problem.

In his textbook Modern Operating Systems (Prentice-Hall, 1992) Tannenbaum gives the pseudo-code for a solution to the dining philosophers problem that is shown below. Similar solutions are found in most operating systems textbooks. All of them are renditions of the original treatment by Dijkstra, which motivated the semaphore mechanism he was introducing in his original article. A \emph{semaphore} is an integer or boolean value, S, with two associated atomic operations:

DOWN(S)	wait until S > 0, then decrement S;
UP(S)	increment S

In time-sharing systems, "waiting" is implemented by the operating system, which may put processes on a wait-list for later execution. In hardware, "waiting" may be accomplished by busy-waiting or by some form of explicit signaling, such as token passing.

Tannenbaum's Solution. This solution uses only boolean semaphors. There is one global semaphore to provide mutual exclusion for exectution of critical protocols. There is one semaphore for each chopstick. In addition, a local two-phase prioritization scheme is used, under which philosophers defer to their neighbors who have declared themselves "hungry." All arithmetic is modulo 5.

system DINING_PHILOSOPHERS

VAR
me:    semaphore, initially 1;                    /* for mutual exclusion */
s[5]:  semaphore s[5], initially 0;               /* for synchronization */
pflag[5]: {THINK, HUNGRY, EAT}, initially THINK;  /* philosopher flag */

As before, each philosopher is an endless cycle of thinking and eating.

procedure philosopher(i)
  {
    while TRUE do
     {
       THINKING;
       take_chopsticks(i);
       EATING;
       drop_chopsticks(i);
     }
  }

The take_chopsticks procedure involves checking the status of neighboring philosophers and then declaring one's own intention to eat. This is a two-phase protocol; first declaring the status HUNGRY, then going on to EAT.

procedure take_chopsticks(i)
  {
    DOWN(me);               /* critical section */
    pflag[i] := HUNGRY;
    test[i];
    UP(me);                 /* end critical section */
    DOWN(s[i])              /* Eat if enabled */
   }

void test(i)            /* Let phil[i] eat, if waiting */
  {
    if ( pflag[i] == HUNGRY
      && pflag[i-1] != EAT
      && pflag[i+1] != EAT)
       then
        {
          pflag[i] := EAT;
          UP(s[i])
         }
    }

Once a philosopher finishes eating, all that remains is to relinquish the resources---its two chopsticks---and thereby release waiting neighbors.

void drop_chopsticks(int i)
  {
    DOWN(me);                /* critical section */
    test(i-1);               /* Let phil. on left eat if possible */
    test(i+1);               /* Let phil. on rght eat if possible */
    UP(me);                  /* up critical section */
   }

The protocol is fairly elaborate, and Tannenbaum's presentation is made more subtle by its coding style.

A Simpler Solution. Other authors, including Dijkstra, have posed simpler solutions to the dining philosopher problem than that proposed by Tannenbaum (depending on one's notion of "simplicity," of course). One such solution is to restrict the number of philosophers allowed access to the table. If there are N chopsticks but only N-1 philosophers allowed to compete for them, at least one will succeed, even if they follow a rigid sequential protocol to acquire their chopsticks.

This solution is implemented with an integer semaphore, initialized to N-1. Both this and Tannenbaum's solutions avoid deadlock a situation in which all of the philosophers have grabbed one chopstick and are deterministically waiting for the other, so that there is no hope of recovery. However, they may still permit starvation, a scenario in which at least one hungry philosopher never gets to eat.

Starvation occurs when the asynchronous semantics may allow an individual to eat repeatedly, thus keeping another from getting a chopstick. The starving philosopher runs, perhaps, but doesn't make progress. The observation of this fact leads to some further refinement of what fairness means. Under some notions of fairness the solutions given above can be said to be correct.