Question
In: Statistics and Probability
At Case Western Reserve University, 46.6% of the student body are undergraduates and 53.4% of those...
At Case Western Reserve University, 46.6% of the student body are undergraduates and 53.4% of those enrolled are graduate students. 60.7% of undergraduate students participate in extracurricular activities, while only 32.1% of graduate students participate in extracurricular activities. A student who participates in extracurricular activities is randomly selected. What is the probability that the student is an undergraduate? Use Baye’s theorem to solve this problem. (Write your answer as a percent rounded to 1 decimal place.)
Solutions
Expert Solution
Solution:
Given: 46.6% of the student body are undergraduates and 53.4% of those enrolled are graduate students.
Let UG = Student is Undergraduates and G = Student is Graduates
Thus we have:
P(UG) = 0.466
P(G) =0.534
60.7% of undergraduate students participate in extracurricular activities.
Let EA = Students participate in Extracurricular Activities.
thus
P(EA | UG) = 0.607
32.1% of graduate students participate in extracurricular activities.
P(EA | G) = 0.321
We have to find:
P( the student is an undergraduate given that student participates in extracurricular activities ) =..........?
P(UG | EA) =..........?
Using Baye’s theorem of probability we get:
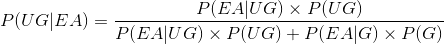
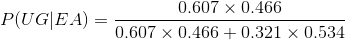
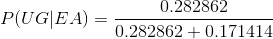
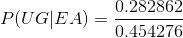

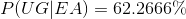

Related Solutions
A Positive Revolution in Change: Appreciative Inquiry David L. Cooperrider Case Western Reserve University and Diana...
at a large University the graduation rate for the general student body was reported to be...
A survey at Evashevski University showed that 75% of the student body believes that the school...
Chapter 15 The University Bookstore Student Computer Purchase Program Case page 762 The University Bookstore Student...
The student body of a large university consists of 30% Business majors. A random sample of...
[6] Sixty percent of the student body at the University of British Columbia is from British...
An Office of Admission document at a certain university claims that 55.3% of their undergraduates are...
In 2015, the student body of a Lock Haven University consisted of 30% freshmen, 24% sophomores,...
***URGENT*** TEST 1. At one large university, freshmen account for the 40% of the student body,...
A study conducted at a major university indicates that the tendency among undergraduates to seek the...
- The score recorded for student 12 for event 5 is incorrect. The score should be a...
- Formulate the outline of a precision pricing policy for a four-star hotel designed to accommodate business...
- The chosen Company is Amazon. Financial statements for the years 2016, 2017 and 2018. A. Analyze...
- With the establishment of the World Trade Organization (WTO) in 1995 (previously General Agreement on Tariffs...
- The London Private Hospital has 3 patient services departments – Adult Medicine, Obstetrics and Paediatrics. It...
- Suppose that an initially empty queue performs the following operations. enqueue(7), enqueue(3), dequeue(), front(), enqueue(8), enqueue(5),...
- Write a program that manages a list of patients for a medical office. Patients should be...
 orchestra answered 3 years ago
orchestra answered 3 years ago