Question

Pulse rates of women are normally distributed with a mean of 77.5 beats per minute and a standard deviation of 11.6 beats per minute. Answer the following questions.

What are the values of the mean and standard deviation after converting all pulse rates of women to z scores using \(\mathrm{z}=\frac{(\mathrm{x}-\mu)}{\sigma}\) ?

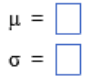
The original pulse rates are measure with units of "beats per minute". What are the units of the corresponding z scores? Choose the correct choice below.

• The z scores are measured with units of "beats per minute".
• The z scores are measured with units of "minutes per beat".
• The z scores are measured with units of "beats."
• The z scores are numbers without units of measurement.

Answer 1

It is given that the pulse rates of women have mean values as 77.5, and the standard deviation is 11.6. All pulse rates are converted into z-scores by subtracting the mean from each of the values and dividing the corresponding result with the standard deviation.

The converted z-scores are as shown below:

$$ \begin{array}{|l|l|l|l|} \hline P U L S E & z-\text {scores} & P U L S E & z-\text {scores} \\ \hline 78 & 0.0431 & 90 & 1.07759 \\ \hline 80 & 0.21552 & 90 & 1.07759 \\ \hline 68 & -0.819 & 68 & -0.819 \\ \hline 56 & -1.8534 & 72 & -0.4741 \\ \hline 76 & -0.1293 & 82 & 0.38793 \\ \hline 78 & 0.0431 & 72 & -0.4741 \\ \hline 78 & 0.0431 & 78 & 0.0431 \\ \hline 90 & 1.07759 & 104 & 2.28448 \\ \hline 96 & 1.59483 & 62 & -1.3362 \\ \hline 60 & -1.5086 & 72 & -0.4741 \\ \hline 98 & 1.76724 & 72 & -0.4741 \\ \hline 66 & -0.9914 & 88 & 0.90517 \\ \hline 100 & 1.93966 & 74 & -0.3017 \\ \hline 76 & -0.1293 & 72 & -0.4741 \\ \hline 64 & -1.1638 & 82 & 0.38793 \\ \hline 82 & 0.38793 & 78 & 0.0431 \\ \hline 62 & -1.3362 & 78 & 0.0431 \\ \hline 72 & -0.4741 & 98 & 1.76724 \\ \hline 74 & -0.3017 & 64 & -1.1638 \\ \hline \end{array} $$

Using MINITAB, the descriptive statistic for the z-scores is as shown below:

From the MINITAB output, \(\mu=0\) and \(\sigma=0.996 \approx 1\)

Here, the pulse rates are measured with given units. But the corresponding z-scores are the numbers or constant. So, the z-scores will not have any units of measurements.

Therefore, the correct option is D.