Question

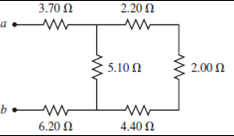
What is the equivalent resistance between points a and b of the six resistors shown in the Figure below?

 

Answer 1

Draw the labeled circuit as shown below.

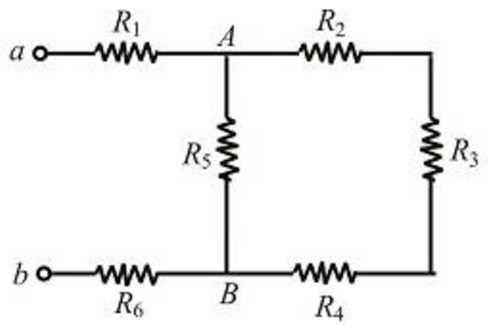
Write the expression for the three resistors connected in series.

$$ R_{e q}=R_{2}+R_{3}+R_{4} $$

Here, \(R_{e q}\) is the equivalent resistance, and \(R_{2}, R_{3}, R_{4}\) are the three resistors connected in series.

Write the expression for the equivalent resistance across branch \(\mathrm{AB}\).

$$ R_{A B}=\frac{R_{5} \times R_{e q}}{R_{5}+R_{e q}} $$

Here, \(R_{A B}\) is the equivalent resistance across branch \(\mathrm{AB}\) and \(R_{5}, R_{e q}\) are the two resistors connected in parallel across points \(\mathrm{AB}\).

Write the expression for the equivalent resistance of the circuit.

$$ R_{e q}^{\prime}=R_{A B}+R_{1}+R_{6} $$

Here, \(R_{e q}^{\prime}\) is the equivalent resistance of the circuit and \(R_{A B}, R_{1}, R_{6}\) are the three resistors connected in series.

Conclusion:

Substitute \(2.20 \Omega\) for \(R_{2}, 2.00 \Omega\) for \(R_{3}, 4.40 \Omega\) for \(R_{4}\) in the equation (I).

$$ \begin{gathered} R_{e q}=(2.20 \Omega)+(2.00 \Omega)+(4.40 \Omega) \\ =8.60 \Omega \end{gathered} $$

Substitute \(8.60 \Omega\) for \(R_{e q}\) and \(5.10 \Omega\) for \(R_{5}\) in the equation (II).

$$ \begin{aligned} R_{A B} &=\frac{(5.10 \Omega) \times(8.60 \Omega)}{(5.10 \Omega)+(8.60 \Omega)} \\ &=\frac{43.86}{13.7} \Omega \\ &=3.20 \Omega \end{aligned} $$

Substitute \(3.70 \Omega\) for \(R_{1}, 3.20 \Omega\) for \(R_{A B}, 6.20 \Omega\) for \(R_{6}\) in the equation (III).

$$ \begin{gathered} R_{e q}^{\prime}=(3.20 \Omega)+(3.70 \Omega)+(6.20 \Omega) \\ =13.1 \Omega \end{gathered} $$

Thus, the equivalent resistance of the circuit is \(13.1 \Omega\).

The equivalent resistance of the circuit is 13.1Ω.