Question

Part D

For the combination of resistors shown, find the equivalent resistance between points A and B.

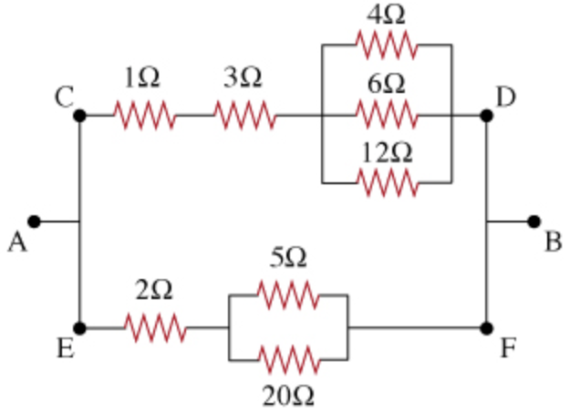
(Figure 6)

Express your answer in Ohms.

Req =

?

Answer 1

Concepts and reason

The concepts used to solve this problem are effective resistance of resistors connected in series and parallel. First, calculate the effective resistance of the resistors in top and bottom branch connected in parallel. Now, the effective resistances of the parallel resistors are in series with the rest of the resistors in their respective branches. Then, calculate the effective resistance of the series combinations of resistors in top and bottom branch. Now, the equivalent resistance of the top and bottom branch will be parallel to each other. Finally, use the formula to calculate the resistance for the resistors connected in parallel to calculate the equivalent resistance of the resistors in top and bottom branch between point \(A\) and \(B\).

Fundamentals

The expression for the equivalent resistance of the resistor connected in series is, \(R_{\mathrm{eq}}=R_{1}+R_{2}\)

Here, \(R_{\mathrm{eq}}\) is the equivalent resistance of the resistors connected in series, \(R_{1}, R_{2}\) are the resistors connected in series.

The expression for the equivalent resistance of the resistor connected in parallel is, \(\frac{1}{R^{\prime} \mathrm{eq}}=\frac{1}{R 3}+\frac{1}{R 4}+\frac{1}{R 5}\)

Here, \(R_{\mathrm{eq}}^{\prime}\) is the equivalent resistance of the resistors connected in parallel, \(R_{3}, R_{4}, R_{5}\) are the resistors connected in parallel.

 

(D) The given combination of resistors can be divided into top and bottom branch of resistors. The top branch resistors are shown in the figure below:

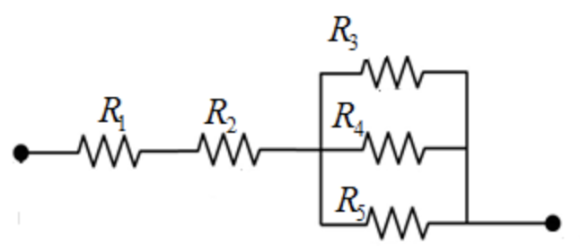
The expression to calculate the equivalent resistance of the resistor connected in parallel to the top branch is, \(\frac{1}{R_{\mathrm{eqt}}^{\prime}}=\frac{1}{R_{3}}+\frac{1}{R_{4}}+\frac{1}{R_{5}}\)

Here, \(R_{\mathrm{eqt}}^{\prime}\) is the equivalent resistance for three resistors connected in parallel to the top branch in the circuit and \(R_{3}, R_{4}, R_{5}\) are the resistors connected in parallel combination. Substitute \(4 \Omega\) for \(R_{3}, 6 \Omega\) for \(R_{4},\) and \(12 \Omega\) for \(R_{5}\) to find \(R_{\mathrm{eqt}}^{\prime}\)

$$ \begin{array}{c} \frac{1}{R_{\text {eqt }}^{\prime}}=\frac{1}{4 \Omega}+\frac{1}{6 \Omega}+\frac{1}{12 \Omega} \\ =\frac{1}{2 \Omega} \\ R_{\text {eqt }}^{\prime}=2 \Omega \end{array} $$

The expression for the equivalent resistance of the resistor connected in series at the top branch is, \(R_{\mathrm{top}}=R_{1}+R_{2}+R_{\mathrm{eqt}}^{\prime}\)

Substitute \(1 \Omega\) for \(R_{1}, 3 \Omega\) for \(R_{2}, 2 \Omega\) for \(R_{\mathrm{eqt}}^{\prime}\)

$$ \begin{array}{c} R_{\mathrm{top}}=1 \Omega+3 \Omega+2 \Omega \\ =6 \Omega \end{array} $$

The effective resistance of the parallel combination of resistors at the top branch is calculated using the expression \(\frac{1}{R^{\prime} \text { eqt }}=\frac{1}{R_{3}}+\frac{1}{R_{4}}+\frac{1}{R_{5}} .\) It is found that the effective resistance of the capacitors connected in parallel is less than the resistance of the individual resistor in that parallel combination. The effective resistance is now in series with the other resistors at the top branch. Finally, the equivalent resistance of the top branch is found using the expression, \(R_{\mathrm{top}}=R_{1}+R_{2}+R_{\mathrm{eqt}}^{\prime}\)

The bottom branch resistors are shown in the figure below:

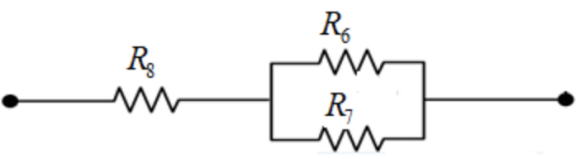
The expression for the equivalent resistance of the resistor connected in parallel at the bottom branch is, \(\frac{1}{R^{\prime} \text { eqb }}=\frac{1}{R 6}+\frac{1}{R 7}\)

Here, \(R_{\mathrm{eqb}}^{\prime}\) is the equivalent resistance for two resistors at the bottom branch of the circuit and \(R_{6}, R_{7}\) are the resistors connected in parallel combination. Substitute \(5 \Omega\) for \(R_{6}\) and \(20 \Omega\) for \(R_{7}\) to find \(R_{\mathrm{eqb}}^{\prime}\)

\(\frac{1}{R^{\prime} \text { eqb }}=\frac{1}{R_{6}}+\frac{1}{R_{7}}\)

\(\frac{1}{R^{\prime} \text { eqb }}=\frac{1}{5 \Omega}+\frac{1}{20 \Omega}\)

\(=\frac{1}{4 \Omega}\)

\(R_{\mathrm{eqb}}^{\prime}=4 \Omega\)

The expression for the equivalent resistance of the resistor connected in series at the bottom branch is, \(R_{\text {bottom }}=R_{\mathrm{eqb}}^{\prime}+R_{8}\)

Substitute \(4 \Omega\) for \(R_{\mathrm{eqb}}^{\prime}\) and \(2 \Omega\) for \(R_{8}\) in the above expression.

\(R_{\text {bottom }}=4 \Omega+2 \Omega\)

\(=6 \Omega\)

Now, the equivalent resistance between point \(A\) and \(B\) is,

 

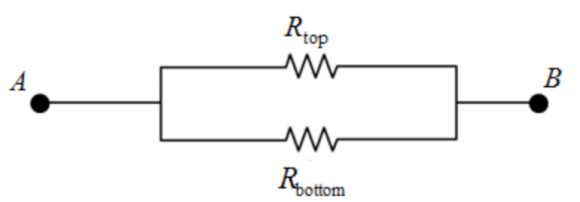
The expression to calculate the equivalent resistance for parallel combination of resistors between point \(\mathrm{A}\) and \(\mathrm{B}\) is, \(\frac{1}{R_{E Q}}=\frac{1}{R_{\mathrm{top}}}+\frac{1}{R_{\mathrm{bottom}}}\)

Substitute \(6 \Omega\) for \(R_{\text {top }}\) and \(6 \Omega\) for \(R_{\text {bottom }}\) in the above expression.

$$ \begin{aligned} \frac{1}{R_{E Q}} &=\frac{1}{6 \Omega}+\frac{1}{6 \Omega} \\ =& \frac{(6 \Omega)(6 \Omega)}{(6 \Omega+6 \Omega)} \\ &=3 \Omega \end{aligned} $$

Part D

Thus, the equivalent resistance between points \(\mathrm{A}\) and \(\mathrm{B}\) is \(3 \Omega\).

The effective resistance of the parallel combination of resistors at the bottom of the circuit is calculated and its effective resistance is found. Finally, the equivalent resistance between points \(\mathrm{A}\) and \(\mathrm{B}\) is calculated using the expression \(\frac{1}{R E Q}=\frac{1}{R_{\text {top }}}+\frac{1}{R \text { bottom }}\)