Question

Company XYZ know that replacement times for the quartz time pieces it produces are normally distributed with a mean of 15.7 years and a standard deviation of 1.2 years.

Find the probability that a randomly selected quartz time piece will have a replacement time less than 13.4 years?
P(X < 13.4 years) =

Enter your answer accurate to 4 decimal places. Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.

If the company wants to provide a warranty so that only 1.5% of the quartz time pieces will be replaced before the warranty expires, what is the time length of the warranty?
warranty =   years

Enter your answer as a number accurate to 1 decimal place. Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.

Answer 1

Given that company XYZ know that replacement times for the quartz time pieces it produces are normally distributed with a mean of 15.7 years and a standard deviation of 1.2 years.

Let,

X=Replacement times for the quartz time pieces

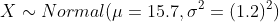
Normal Distribution

A continuous random variable X is said to have a normal distribution if its PDF(Probability Density Function) is given by

its CDF(Cumulative Distribution Function) is given by,

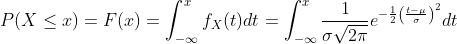
Notation:

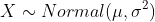
Standard Normal Distribution

A continuous random variable X is said to have a standard normal distribution if its PDF(Probability Density Function) is given by

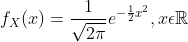
its CDF(Cumulative Distribution Function) is given by,

Exact evaluation of ?(x) is not possible but numerical method can be applied. The values of ?(x) has been tabulated extensively in Biometrika Volume I.

Notation:

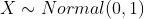
Note:

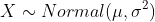
Coming back to our problem

Let,

X=Replacement times for the quartz time pieces

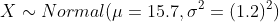
(a) Here we need to find the probability that a randomly selected quartz time piece will have a replacement time less than 13.4 years.

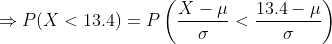
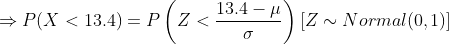
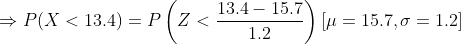
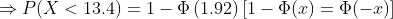
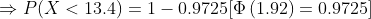
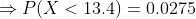
Hence the probability that a randomly selected quartz time piece will have a replacement time less than 13.4 years is 0.0275

(b) Here we need to find the length of the warranty if the company wants to provide a warranty so that only 1.5% of the quartz time pieces will be replaced before the warranty expires.

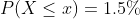
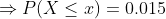
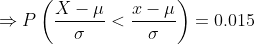
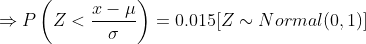
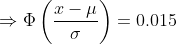
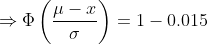
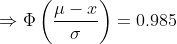
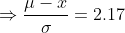
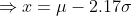
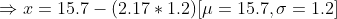
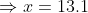
Hence the length of the warranty is 13.1 years.