Question

Demand for oil changes at​ Garcia's Garage has been as​ follows:                                                                 

Month	Number of Oil Changes
January	33
February	53
March	56
April	58
May	69
June	46
July	62
August	69

a. Use simple linear regression analysis to develop a forecasting model for monthly demand. In this​ application, the dependent​ variable, Y, is monthly demand and the independent​ variable, X, is the month. For​ January, let X=​1; for​ February, let X=​2; and so on.

The forecasting model is given by the equation

Y= ___ + ____X.

​(Enter your responses rounded to two decimal​ places.)

Answer 1

Month period(X) demand(Y) XY X^2(square of x)

January 1 33 33 1

February 2 53 106 4

March 3 56 168 9

April 4 58 232 16

May 5 69 345 25

June 6 46 276 36

July 7 62 434 49

August 8 69 552 64

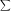X = 1+2+3+4+5+6+7+8 = 36

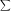Y = 33+53+56+58+69+46+62+69 = 446

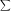XY = 33+106+168+232+345+276+434+552 = 2146

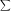X^2 = 1+4+9+16+25+36+49+64 = 204

n = Number of periods = 8

X-bar = 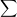X / n = 36/8 = 4.5

Y-bar = 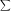Y/n = 446/8 = 55.75

b = ( 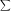XY - nX-bar .Y-bar ) / ( 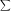X^2 - n. Square of X-bar)

= [2146 - (8)(4.5)(55.75) ] / [204 - (8)(4.5)(4.5)]

= (2146 - 2007) / (204 - 162)

= 139/ 42

= 3.31

a = Y-bar - b(X-bar) = 55.75 - 3.31(4.5) = 55.75 - 14.895 = 40.86

Y = a + bx => Y = 40.86 + 3.31x

So the trend line is Y = 40.86 + 3.31x