Question

Trucks are required to pass through a weighing station so that they can be checked for weight violations. Trucks arrive at the station at the rate of 35 an hour between 7:00 p.m. and 9:00 p.m. Currently two inspectors are on duty during those hours, each of whom can inspect 25 trucks an hour.
Use Table 1.

a. How many trucks would you expect to see at the weighing station, including those being inspected? (Round your answer to 3 decimal places.)

L_s             trucks

b.If a truck was just arriving at the station, about how many minutes could the driver expect to be at the station? (Round your answer to 2 decimal places.)

W_s             min.

c. What is the probability that both inspectors would be busy at the same time?(Round your answer to 4 decimal places.)

P_w           

d. How many minutes, on average, would a truck that is not immediately inspected have to wait? (Round your answer to the nearest whole number.)

W_a             min.

f. What is the maximum line length for a probability of .97? (Round up your answer to the next whole number.)

L _max          

Answer 1

Multiple-Server Model:

Arrival rate, 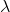= 35 trucks per hour.

Service rate, 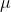= 25 trucks per hour.

Average number of trucks being inspected = 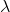/ 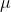= 35 / 25 = 1.4

Number of Servers, M = 2.

For M = 2 and (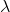 / 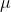) = 1.4 (From Table),

Average number of trucks waiting in line for service, Lq = 1.345  

a.

Average number of trucks in the system = Ls = Lq + (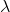 / 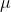) = 1.345 + 1.4 = 2.745

Average number of trucks that would be expected to be seen at the weighing station, including those being inspected, Ls = 2.745 trucks.

b.

Average time trucks are in the system, Ws = (Lq / 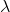) + (1 / 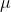) = (1.345 / 35) + (1 / 25) = 0.078 hour = 4.68 minutes.

The number of minutes the driver could be expected to be at the station, Ws = 4.68 minutes.

c.

Average time trucks are waiting in the line, Wq = Lq / 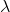= 1.345 / 35 = 0.0384 hours.

Wa = [1 / (M. 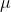- 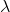) = [ 1 / (2 x 25 – 35)] = 0.07 hours.

Probability that both the inspectors would be busy at the same time, Pw = Wq / Wa = 0.0384 / 0.07 = 0.5486

d.

The number of minutes, on an average, that a truck which is not immediately inspected, has to wait, Wa = [1 / (M. 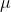- 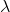) = [ 1 / (2 x 25 – 35)] = 0.067 hours = 4.02 minutes  4 minutes.

f.

System utilization, 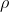= 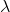/ M. 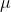= 35 / (2 x 25) = 0.7

K = (1 – Specified Percentage) / Lq.(1 – 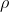) = (1 – 0.97) / [1.345 x (1 – 0.7)] = 0.0743

Lmax = ln K / ln 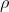= ln 0.0743 / ln 0.7 = 7.28   8 trucks.

Maximum line length, Lmax = 8 trucks.