Question

Imagine someone has created new shoe technology and would like to be able to say that their shoes have led to faster event times. Imagine the data represents Men’s 400 meter freestyle times with the new shoes. Compare against the industry rival’s reported mean time of 4.13 minutes. Complete a one-tailed hypothesis test at the 5% significance level for a single mean to determine if the new suits are statistically faster (hint: is a faster time a smaller or larger time?).

Data Set: 400 Meter Race Times

3.77, 3.51, 3.91, 4.49, 3.71, 3.97, 3.43, 4.47, 3.74, 3.77, 4.08, 4.31, 4.27, 4.17, 3.90, 4.36, 3.84,3.70, 3.68, 4.14, 3.85, 3.86, 3.80, 4.09, 4.03, 4.65, 3.50, 4.54, 4.27, 4.61, 3.89, 4.23, 4.46, 3.84, 3.63, 3.99, 3.88, 3.97, 3.51, 4.62

1. What is the null hypothesis?
2. What is the alternative hypothesis?
3. What is the critical value of the t statistic (use degrees of freedom = 40 as being close enough)?
4. What is the test statistic (a.k.a. calculated value of the t-statistic) from the data set?
5. What is your decision?
6. What is your conclusion?

Answer 1

Create the following table.

data	data-mean	(data - mean)2
3.77	-0.241	0.058081
3.51	-0.501	0.251001
3.91	-0.101	0.010201
4.49	0.479	0.229441
3.71	-0.301	0.090601
3.97	-0.041	0.001681
3.43	-0.581	0.337561
4.47	0.459	0.210681
3.74	-0.271	0.073441
3.77	-0.241	0.058081
4.08	0.069	0.004761
4.31	0.299	0.089401
4.27	0.259	0.067081
4.17	0.159	0.025281
3.90	-0.111	0.012321
4.36	0.349	0.121801
3.84	-0.171	0.029241
3.70	-0.311	0.096721
3.68	-0.331	0.109561
4.14	0.129	0.016641
3.85	-0.161	0.025921
3.86	-0.151	0.022801
3.80	-0.211	0.044521
4.09	0.079	0.006241
4.03	0.019	0.000361
4.65	0.639	0.408321
3.50	-0.511	0.261121
4.54	0.529	0.279841
4.27	0.259	0.067081
4.61	0.599	0.358801
3.89	-0.121	0.014641
4.23	0.219	0.047961
4.46	0.449	0.201601
3.84	-0.171	0.029241
3.63	-0.381	0.145161
3.99	-0.021	0.000441
3.88	-0.131	0.017161
3.97	-0.041	0.001681
3.51	-0.501	0.251001
4.62	0.609	0.370881

Find the sum of numbers in the last column to get.

Here null hypothesis is

Alternative hypothesis is

Test statistics is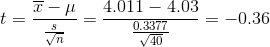

T-Value (right-tailed): 1.6849

As t critical is greater than t statistics we fail to reject the null hypothesis

Hence we conclude that the new suits are not statistically faster