Question

Find the electric field vector anywhere in the plane of a dipole. Let the charge value on one
charge be q. Let them be separated by d. Let the origin be in between them. And say they are
each on the y axis.

Please include a diagram in your answer

Answer 1

• Finding the electric field associated with a dipole anywhere on a plane[edit]

  Now that you've solved for two special cases and determined that the dipole field falls off as at great distances (referred to as the far field), it is instructive to find the field's behavior off the axis.

  Consider the case of an electric dipole's field at a point with the coordinates 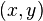as represented in the figure. Note that we can represent the coordinates either as Cartesian, or as cylindrical.

  

  

  dipole field in a plane.

  

  

  
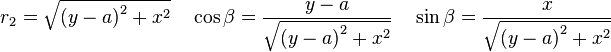
  In Cartesian coordinates the electric field at any point in the plane from each charge can be found as follows:

  

  
  We can apply the principle of superposition and add the fields from each of the charges, remembering that they are vectors so that the vertical components add to vertical and horizontal add to horizontal.

  First finding the horizontal coordinates labeled as :

  

  

  
  Next finding the vertical components for each of the two charges labeled as we obtain:

  

  

  Summing the horizontal components yields:

  

  
  And for large r (either large x, large y, or their combination) this becomes:

  

  
  Summing the vertical components yields: