Question
In: Statistics and Probability
How do you decide whether to reject or fail to reject the null hypothesis? How do...
How do you decide whether to reject or fail to reject the null hypothesis?
How do you tell whether the test is left, right, or two tailed?
Why can we never accept the null hypothesis?
Why does decreasing the probability of making a type one error increase the probability of making a type two error?
How does a researcher decide the level of significance for a hypothesis test?
Solutions
Expert Solution
- In testing of hypothesis, after observing the data, we make inference about our population. In testing of hypothesis, we set our null and alternative hypothesis. Then, we construct a test statistic. The distribution of test-statistic is known when null hypothesis is true. Then, from the observed sample, we calculate the value of our test-statistic. Then, based on our level of significance, we find the critical region. We reject our null hypothesis if the value of test-statistic falls in the critical region. Otherwise, we fail to reject null hypothesis.
- A test whether it is left, right r two-tailed is completely
dependent on the nature of the alternative hypothesis. It will be
very clear when by the following example. Suppose, we test a
conjecture about the mean(
 )
of a population of interest. Let's say historically,
)
of a population of interest. Let's say historically,  . Then we might be interested in knowing whether
. Then we might be interested in knowing whether 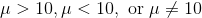 against the null hypothesis that
against the null hypothesis that  , then, if the
, then, if the 
- The test of hypothesis is designed such a way that, if there is significant evidence to claim the rejection of null hypothesis, then we say null is rejected. But, if there is no evidence, i.e the sample does not fall in the rejection region, that means there is no strong evidence in favor of alternative, but that does not mean null is true, it might or might not be true.
- As discussed earlier, the decision of accepting or rejecting
the null hypothesis is dependent on the criticial region or
rejection region. Let
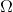 be the entire sample space and R be the rection region. i.e if the
sample falls inside R we will reject null otherwise we will fail to
reject null. Now, type I error means probability of rejecting null
when it is true. Now, if we shrink the rejection region R then, the
probability that we reject null will decrease and automatically we
will decrease the probability of type-I error. But, on the other
hand, shrinking R means we will enlarging the accepting region i.e.
be the entire sample space and R be the rection region. i.e if the
sample falls inside R we will reject null otherwise we will fail to
reject null. Now, type I error means probability of rejecting null
when it is true. Now, if we shrink the rejection region R then, the
probability that we reject null will decrease and automatically we
will decrease the probability of type-I error. But, on the other
hand, shrinking R means we will enlarging the accepting region i.e.
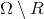 , which means we increase the probability of not rejecting null,
which in turn increases the probability of type-II error.
, which means we increase the probability of not rejecting null,
which in turn increases the probability of type-II error. - The level of significane is the probability of type-I error, i.e probability of false rejection of null hypothesis. Based on situation, depending on how much risk the researcher can take of falsely rejecting null, and depending on its impact, they decides the level of significance as 5%, 10% or 1%.
Related Solutions
What specifically is used to decide whether to reject or fail to reject the null hypothesis?...
What specifically is used to decide whether to reject or fail
to reject the null hypothesis? [1 sentence]
How do you tell whether the test is left, right, or two tailed?
[3 bullets]
A student calculates a p-value and tells you the answer is
2.33. Explain why this could not be correct. [2 sentences]
Why can we never accept the null hypothesis? [2 sentences]
Why does decreasing the probability of making a type one error
increase the probability of making...
For the following questions, state whether you would reject or fail to reject the null hypothesis:...
For the following questions, state whether you would reject or
fail to reject the null hypothesis:
Critical value z > 1.96 or z < -1.96
Test value: -2.87
Critical value z > 2.33
Test value: 1.85
Critical value z > 2.33
Test value: -2.87
Two tailed z test with an α=0.05
Test value: 1.85
One tailed z test in the positive direction with an α=0.01
Test value: 8.56
For the following questions, state whether you would reject or fail to reject the null hypothesis:...
For the following questions, state
whether you would reject or fail to reject the null hypothesis:
Critical value z > 1.96 or z < -1.96
Test value: -2.87
Critical value z > 2.33
Test value: 1.85
Critical value z > 2.33
Test value: -2.87
Two tailed z test with an α=0.05
Test value: 1.85
One tailed z test in the positive direction with an α=0.01
Test value: 8.56
How do we determine if we reject or fail to reject a null hypothesis? What are...
How do we determine if we reject or fail to reject a null
hypothesis?
What are the key pieces needed when writing a conclusion?
How do we determine if we reject or fail to reject a null hypothesis? What are...
How do we determine if we reject or fail to reject a null
hypothesis?
What are the key pieces needed when writing a conclusion?
Suppose I’m trying to determine whether to reject or fail to reject the null hypothesis that...
Suppose I’m trying to determine whether to reject or fail to
reject the null hypothesis that the country has less than or equal
to 70% of people that believe the country is going in the wrong
direction. If this is not true then I hypothesize that it could be
larger than 70%. I’ve also taken a survey of size 50 and have found
the sample percentage to be 75%. My alpha value is .05.
1. Write the null and alternative...
The decision in any hypothesis is to reject the null hypothesis OR to fail to reject...
The decision in any hypothesis is to reject the null hypothesis
OR to fail to reject the null hypothesis.
Under what conditions do you reject the null hypothesis in any
hypothesis test?
Find an example of a hypothesis test of the mean in your
homework this week and use it to explain how a conclusion is
written if the null hypothesis is rejected?
Find an example of a hypothesis test of the mean in your
homework this week and use...
What does it mean to reject or fail to reject the null hypothesis and when do...
What does it mean to reject or fail to reject the null
hypothesis and when do I reject or fail to reject the null
hypothesis?
True or False A. In hypothesis testing, if you fail to reject the null hypothesis, then...
True or False
A. In hypothesis testing, if you fail to reject the null
hypothesis, then you have proven the null hypothesis to be
true.
B. If you are more concerned about a type I error than a type II
error in a hypothesis test, it would be better to use ∝= .01 than
∝= .10.
C. If you have complete information for a population (from a
census), it would be unnecessary and inappropriate to carry out a
hypothesis test...
Using minitab, how do you know whether or not to reject the null hypothesis when you...
Using minitab, how do you know whether or not to reject the null
hypothesis when you are doing a chi-square test for differences
among more than two proportions?
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- The average resident has a demand for fresh oranges which is a linear function of the...
- Fundamentals Of Analytical Chemistry 9th Edition - Skoog Balance the net ionic equation of the following...
- Please use Java only. Write the class TopResult, which keeps track of the best (highest numbered...
- Define the equivalence point of an acid-base titration. Describe it for a weak acid-strong base titration...
- In the following problem, check that it is appropriate to use the normal approximation to the...
- Van Rushing Hunting Goods’ fiscal year ends on December 31. At the end of the 2021...
- A business has 10 employees. Their annual wages (to the nearest thousands of dollars) are as...
ADVERTISEMENT
 )
of a population of interest. Let's say historically,
)
of a population of interest. Let's say historically,  . Then we might be interested in knowing whether
. Then we might be interested in knowing whether 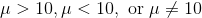 against the null hypothesis that
against the null hypothesis that 
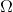 be the entire sample space and R be the rection region. i.e if the
sample falls inside R we will reject null otherwise we will fail to
reject null. Now, type I error means probability of rejecting null
when it is true. Now, if we shrink the rejection region R then, the
probability that we reject null will decrease and automatically we
will decrease the probability of type-I error. But, on the other
hand, shrinking R means we will enlarging the accepting region i.e.
be the entire sample space and R be the rection region. i.e if the
sample falls inside R we will reject null otherwise we will fail to
reject null. Now, type I error means probability of rejecting null
when it is true. Now, if we shrink the rejection region R then, the
probability that we reject null will decrease and automatically we
will decrease the probability of type-I error. But, on the other
hand, shrinking R means we will enlarging the accepting region i.e.
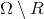 , which means we increase the probability of not rejecting null,
which in turn increases the probability of type-II error.
, which means we increase the probability of not rejecting null,
which in turn increases the probability of type-II error. orchestra answered 3 years ago
orchestra answered 3 years ago