1 (a). Examine. with practicals examples, the general form of a particle undergoing sinmple harmonic motion...

1 (a). Examine. with practicals examples, the general form of a particle undergoing sinmple harmonic motion and carefully explain all the associated terms

Solutions

Expert Solution

simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement.

Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law

Mathematically, the restoring force F is given by

where F is the restoring elastic force exerted by the spring (in SI units: N), k is the spring constant (N·m⁻¹), and x isthe displacement from the equilibrium position (in m).

For one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, can be obtained by means of Newton's second law (and Hooke's law for a mass on a spring).

where m is the inertial mass

The kinetic energy K of the system at time t is

and the potential energy is

Mass of a simple pendulum The period of a mass attached to a pendulum of length ℓ with gravitational acceleration g is given by

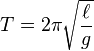
genius_generous answered 2 weeks ago

Next > < Previous

Related Solutions

particle is in simple harmonic motion along the x axis. The amplitude of the motion is...

particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. When it is at x = x1, its kinetic energy is K = 5 J and its potential energy (measured with U = 0 at x = 0) is U = 3 J. When it is at x = −1 2x1, the kinetic and potential energies are: A. K = 5 J and U = 3J B. K = 5 J and U...

A particle executes simple harmonic motion, such that at a given time, it is at ?A/3...

A particle executes simple harmonic motion, such that at a given time, it is at ?A/3 moving in towards equilibrium. 0.7seconds later, it is at x=0.9A moving towards equilibrium. Find the angular frequency of the particle, if it passes through equilibrium once between the two occurrences. Repeat the above, with the particle passing through equilibrium 5times between the two occurrences.

1. A particle undergoing circular motion in the xy-plane stops on the negative x-axis. Which of...

1. A particle undergoing circular motion in the xy-plane stops on the negative x-axis. Which of the following does not describe the angular position? a) 4π radians b) π radians c) 5π radians d) 3π radians 2. Two balls collide. The first ball (mass 3 kg) reaches a speed of 40 m/s before the collision. After the collision, the first ball has stopped and the second ball (mass 3 kg) travels at 40 m/s. What was the initial velocity of...

(A particle that vibrates under the influence of a simple harmonic motion) If the total energy...

(A particle that vibrates under the influence of a simple harmonic motion) If the total energy is greater than the effort - solve the Schrödinger equation using polynomial Hermit

And object is undergoing simple harmonic motion along the x-axis. Its position is described as a...

And object is undergoing simple harmonic motion along the x-axis. Its position is described as a function of time by x(t) = 2.7 cos(3.1t – 1.2), where x is in meters, the time, t, is in seconds, and the argument of the cosine is in radians. A) Find the amplitude of the simple harmonic motion, in meters. B) What is the value of the angular frequency, in radians per second? C) Determine the position of the object, in meters, at...

An object is undergoing simple harmonic motion along the x-axis. Its position is described as a...

An object is undergoing simple harmonic motion along the x-axis. Its position is described as a function of time by x(t) = 5.5 cos(6.9t – 1.1), where x is in meters, the time, t, is in seconds, and the argument of the cosine is in radians. Part (a) Find the amplitude of the simple harmonic motion, in meters. 14% Part (b) What is the frequency of the motion, in hertz? 14% Part (c) Determine the position of the object, in...

Consider a particle that is conﬁned by a one dimensional quadratic (harmonic) potential of the form...

Consider a particle that is conﬁned by a one dimensional quadratic (harmonic) potential of the form U(x) = Ax2 (where A is a positive real number). a) What is the Hamiltonian of the particle (expressed as a function of velocity v and x)? b) What is the average kinetic energy of the particle (expressed as a function of T)? c) Use the Virial Theorem (Eq. 1.46) to obtain the average potential energy of the particle. d) What would the average...

Lab 12- SIMPLE HARMONIC MOTION PRELAB QUESTIONS 1) Explain Hooke’s Law. 2) What two examples of...

Lab 12- SIMPLE HARMONIC MOTION PRELAB QUESTIONS 1) Explain Hooke’s Law. 2) What two examples of harmonic oscillators will we examine in this lab? Explain the forces acting on each. 3) How does the total mechanical energy in the oscillating system change as it oscillates? 4) Calculate the frequency of oscillation for a 3 meter long simple pendulum swinging on the Moon, where g= 1.62 m/s2. Calculate the frequency of oscillation for a 3 meter long simple pendulum swinging on...

This problem is an example of critically damped harmonic motion.

This problem is an example of critically damped harmonic motion. A mass m=6kg is attached to both a spring with spring constant k=96N/m and a dash-pot with damping constant c=48N⋅s/m . The ball is started in motion with initial position x0=5m and initial velocity v0=−24m/s . Determine the position function x(t) in meters. x(t)= Graph the function x(t) . Now assume the mass is set in motion with the same initial position and velocity, but with the dashpot disconnected (...

Write a discussion and conclusion for simple harmonic motion.

Subjects