Question

Ron Swanson is by his fireplace drinking his favorite Lagavulin scotch (the 16 year, of course). He pours 2 ounces (60 ml) of scotch taken from ambient temperature (20°C) and adds 2 cubes of ice, each weighing 1 g that are initially at 0°C. What is the final temperature of the scotch after the ice has melted and equilibrium has been reached? Include a heat diagram in your solution. Density of scotch = 950 kg/m3 Specific heat capacity: scotch 2000 J/(kg°C); water 4186 J/(kg°C) Latent heat of fusion for ice/water: 3.33 x 105 J/kg Important Note: you do NOT need to convert to K. If you use °C, the answer you will get will be in °C; if you convert to K, the answer you will get will be in K.

Answer 1

GIven,

Density of scotch, 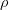= 950 kg/m³ = [ 950*(10³/10⁶) ] g/cm³

                                 = 0.95 g/cm³

Volume of scotch, V = 60 ml

Since, 1 ml = 1 cm³

=> V = 60 cm³

Let mass of scotch be m

=> m = 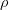*V = 0.95 * 60 = 57 g

Now,

mass of ice, m' = 2 g

Now,

heat capacity of scotch, c_s = 2000 J/kgC = 2 J/gC

heat capacity of water, c_w = 4186 J/kgC = 4.186 J/gC

latent heat of fusion, L = 3.33 * 10⁵ J/kgC = 333 J/gC

Initial temperature, T = 20 C

Let the final temperature be T'

Now,

Heat lost by scotch in reaching the equilibrium temperature = latent heat needed to convert ice into water

                                                                                                + heat needed to raise the temperature from 0 to T

=> m*c_s*(20 - T) = m'*L + m'*c_w*(T - 0)

=> 57*2*(20 - T) = 2*333 + 2*4.186*T

=> 2280 - 114*T = 666 + 8.372*T

=> 114*T + 8.372*T = 2280 - 666 = 1614

=> 122.372*T = 1614

=> T = 1614 / 122.372

         = 13.2 C

Thus, equlibrium temperature is 13.2 C