Question

The scores on a nationwide wide Principles of Psychology exam are normally distributed, with population mean = 70 and population standard deviation = 12. Use this information to answer the following:

1. The percentile rank for a score of 85 (5pts)

2. The percentage of scores that fall beyond (above) a score of 75 (5pts)

3. A statistician took a sample of, N=55, persons. The MEAN Principles of Psychology exam score for this sample was 80. Using the information in question 3 determine the percentage of MEAN scores that fall below the mean exam score (80). (8pts)

4. What is the standard error of the MEAN Principles of Psychology exam score? (2pts)
   Tip! Before answering each question, draw a diagram of the normal curve to show the position(s) of

   the score(s) in question

Answer 1

Solution:
Given: The scores on a nationwide wide Principles of Psychology examination are normally distributed, with population mean = 70 and population standard deviation = 12.

That is: X ~ Normal(

Part a) The percentile rank for a score of 85

That is find:

P( X < 85)= ......?

Find z score:

Thus we get:

P( X < 85)= P(Z <1.25)

Look in z table for z = 1.2 and 0.05 and find corresponding area.

Thus from z table , we get:
P( Z < 1.25) = 0.8944

Thus

P( X < 85)= P(Z <1.25)

P( X < 85)= 0.8944

Thus the percentile rank for a score of 85 is 89.44%

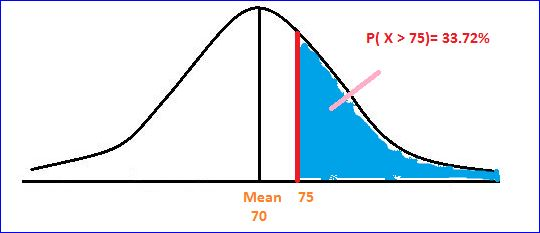
Part b) The percentage of scores that fall beyond (above) a score of 75

That is:

P( X> 75 ) =............?

Find z score:

Thus we get:

P( X> 75 ) = P( Z > 0.42)

P( X> 75 ) = 1 - P( Z < 0.42)

Look in z table for z = 0.4 and 0.02 and find area.

Thus from z table , we get:

P( Z< 0.42 ) = 0.6628

Thus

P( X> 75 ) = 1 - P( Z < 0.42)

P( X> 75 ) = 1 - 0.6628

P( X> 75 ) = 0.3372

P( X> 75 ) = 33.72 %

Thus the percentage of scores that fall beyond (above) a score of 75 is 33.72%

Part c)

Sample size = N = 55

Sample mean =

We have to find: the percentage of MEAN scores that fall below the mean exam score (80).

That is:

Thus find z score:

thus we get:

Since z = 6.18 is very large z value, so area under z = 6.18 is approximately 1

That is: P( Z < 6.18) = 1.0000 =100%

Part d) What is the standard error of the MEAN Principles of Psychology exam score?

Standard Error: