Question

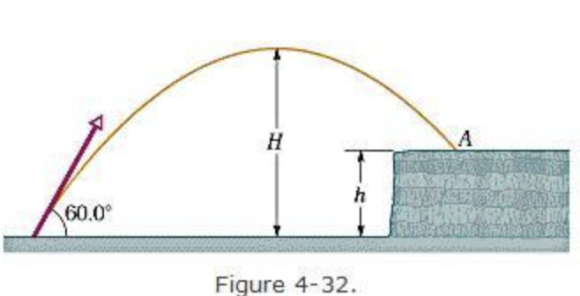
A stone is projected at a cliff of height h with an initial speed of 42.0 m/s directed 60.0° above the horizontal, as shown in Fig. 4-32. The stone strikes at A, 5.50 s after launching.

Find:
(a) the height h of the cliff,
_______ m
(b) the speed of the stone just before impact at A, and
_________ m/s
(c) the maximum height H reached above the ground.
__________ m

Answer 1

Concepts and reason

The concepts used to solve the question is the projectile motion and the equations of the motion. At first, determine the horizontal and vertical components of the velocity and then apply the motion equations to determine the cliff's height, speed of the stone, and maximum height reached by the stone from the ground.

Fundamentals

Projectile motion A projectile is any object upon which only force acts as the force of gravity. When a stone is thrown upwards, the force of gravity is acting downwards. Thus, the object is moving upwards and slowing down. Hence, gravity causes a vertical acceleration, which pulls the object in a downward direction. Equations of motion The equations describing the motion of the objects concerning the time are defined as the kinematic equations. These equations are used when there is constant acceleration. Constant acceleration means that the speed of the object is changing uniformly. Constant acceleration does not mean that the speed of the object is constant. If the speed of the object is constant, then there will be zero acceleration. The equations of the motion are described below. \(v=u+a t\)

Here, \(v\) is the final velocity, \(u\) is the initial velocity, \(a\) is the acceleration of the object and \(t\) is the time taken. The displacement equation is, \(S=u t+\frac{a t^{2}}{2}\)

And \(v^{2}=u^{2}+2 a S\)

(a) The vertical component of the velocity of stone is, \(v_{\mathrm{y}}=v_{0} \sin \theta \ldots \ldots(1)\)

Here, \(v_{0}\) is the initial velocity of the stone and \(\theta\) is the angle of the projection. Substitute \(42 \mathrm{~m} / \mathrm{s}\) for \(v_{0}\) and \(60^{\circ}\) for \(\theta\) in the equation (1)

$$ \begin{aligned} & v_{\mathrm{y}}=v_{0} \sin \theta \\ =&(42 \mathrm{~m} / \mathrm{s}) \sin 60^{\circ} \\ &=36.373 \mathrm{~m} / \mathrm{s} \end{aligned} $$

The horizontal component of the velocity of the stone is, \(v_{\mathrm{x}}=v_{0} \cos \theta \ldots \ldots(2)\)

Substitute \(42 \mathrm{~m} / \mathrm{s}\) for \(v_{0}\) and \(60^{\circ}\) for \(\theta\) in the equation (2)

$$ v_{\mathrm{x}}=v_{0} \cos \theta $$

\(=(42 \mathrm{~m} / \mathrm{s}) \cos 60^{\circ}\)

$$ =21 \mathrm{~m} / \mathrm{s} $$

Apply the equation of the motion to determine the height of the cliff. \(h=v_{\mathrm{y}} t-\frac{g t^{2}}{2} \ldots \ldots(3)\)

Here, \(g\) is the acceleration due to gravity. Substitute, \(36.373 \mathrm{~m} / \mathrm{s}\) for \(v_{\mathrm{y}}, 5.50 \mathrm{~s}\) for \(t\) and \(9.81 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) in the equation (3)

$$ \begin{array}{c} h=(36.373 \mathrm{~m} / \mathrm{s})(5.50 \mathrm{~s})-\frac{\left(9.81 \mathrm{~m} / \mathrm{s}^{2}\right)(5.50 \mathrm{~s})^{2}}{2} \\ =51.675 \mathrm{~m} \end{array} $$

(b) The final velocity along the horizontal direction is,

$$ v_{\mathrm{f} x}=v_{\mathrm{x}} $$

\(=21 \mathrm{~m} / \mathrm{s}\)

The final velocity of the stone along the vertical direction is, \(v_{\mathrm{fy}}=v_{\mathrm{y}}-g t \ldots \ldots(4)\)

Substitute, \(36.373 \mathrm{~m} /\) sfor \(v_{\mathrm{y}} 5.50 \mathrm{~s} t\) and \(9.81 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) in the equation (4)

$$ \begin{array}{c} v_{\mathrm{fy}}=v_{\mathrm{y}}-g t \\ =(36.373 \mathrm{~m} / \mathrm{s})-\left(9.81 \mathrm{~m} / \mathrm{s}^{2}\right)(5.50 \mathrm{~s}) \\ =-17.582 \mathrm{~m} / \mathrm{s} \end{array} $$

The speed of the stone just before the impact at point \(\mathrm{A}\) is,

$$ v=\sqrt{v_{\mathrm{fx}}^{2}+v_{\mathrm{fy}}^{2}} $$

\(=\sqrt{(21 \mathrm{~m} / \mathrm{s})^{2}+(-17.582 \mathrm{~m} / \mathrm{s})^{2}}\)

$$ =27.388 \mathrm{~m} / \mathrm{s} $$

(c) The maximum height of the stone is, \(H=\frac{v_{\mathrm{fy}}^{2}-v_{\mathrm{y}}^{2}}{-2 g} \ldots \ldots\) (5)

Substitute \(0 \mathrm{~m} /\) sfor \(v_{\mathrm{fy}}, 36.373 \mathrm{~m} / \mathrm{s}\) for \(v_{\mathrm{y}}\) and \(9.81 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\) in the equation (5)

$$ \begin{array}{c} H=\frac{v \mathrm{fy}^{2}-v_{\mathrm{y}}^{2}}{-2 g} \\ =\frac{(0 \mathrm{~m} / \mathrm{s})^{2}-(36.373 \mathrm{~m} / \mathrm{s})^{2}}{-2\left(9.81 \mathrm{~m} / \mathrm{s}^{2}\right)} \\ =67.430 \mathrm{~m} \end{array} $$