Question

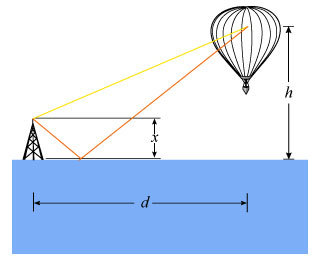
A radar tower sends out a signal of wavelength λ. It is x meters tall, and it stands on the edge of the ocean. A weather balloon is released from a boat that is a distance d out to sea. The balloon floats up to an altitude h.In this problem, assume that the boat and balloon are so far away from the radar tower that the small angle approximation holds.

a) Due to interference with reflections off the water, certain wavelengths will be weak when they reach the balloon. What is the maximum wavelength λ that will interfere destructively?

b) What is the maximum wavelength λ that will interfere constructively?

A radar tower sends out a signal of wavelength lambda. It is x meters tall, and it stands on the edge of the ocean. A weather balloon is released from a boat that is a distance d out to sea. The balloon floats up to an altitude h.In this problem, assume that the boat and balloon are so far away from the radar tower that the small angle approximation holds. 

 a) Due to interference with reflections off the water, certain wavelengths will be weak when they reach the balloon. What is the maximum wavelength lambda that will interfere destructively? 

b) What is the maximum wavelength lambda that will interfere constructively?

Answer 1

Concepts and reason

The concepts used to solve this problem are constructive interference and destructive interference.

According to the principle of super position when several light waves coincide the result is equal to the sum of individual waves.

Use the condition for the destructive interference to find the value of maximum wavelength that will interfere destructively.

Then use the condition for the constructive interference to find the value of maximum wavelength that will interfere constructively.

Fundamentals

If two waves of same wavelength and phase travel different distances to reach the same point their interference will be two types.

Constructive, if difference in path length is integer number of wavelengths.

Destructive, if difference in path length is half integer number of wavelength.

Condition for constructive interference is,

Here, is the separation distance between two slits, is the angle from the midline to the spot on the balloon, is the integer, and is the wavelength.

Condition for destructive interference is,

(a)

Condition for destructive interference is,

…… (1)

From the figure the value of is,

Here, is the altitude of the balloon and is the horizontal distance between tower and balloon.

The value of is much greater than then the equation becomes,

Substitute for , for , and for in equation (1).

Here, is the distance between the two rays.

Therefore, the maximum wavelength that will interfere destructively is .

(b)

Condition for constructive interference is,

Substitute for , for , and for in equation (1).

Therefore, the maximum wavelength that will interfere constructively is .

Ans: Part a

The maximum wavelength that will interfere destructively is .

The maximum wavelength that will interfere constructively is .