Question

1. Let X and Y equal the number of milligrams of tar in filtered and nonfiltered cigarettes, respectively. Assume that ?~?(?_?, ?²) and ?~?(?_?, ?²). We shall test the null hypothesis ?₀: ?_? = ?_? against the alternative hypothesis ?_?: ?_? < ?_? using independent random samples of sizes n = 9 and m = 11 observations from X and Y, respectively.
   1. Define the test statistic for testing the above hypothesis, and the rejection region that is associated with an ? = 0.01 significance level. Sketch a figure illustrating this rejection region.
   2. Given the n = 9 observations on X: 0.9, 1.1, 0.1, 0.7, 0.4, 0.9, 0.8, 1.0, 0.4; and the m = 11 observations on Y: 1.5, 0.9, 1.6, 0.5, 1.4, 1.9, 1.0, 1.2, 1.3, 1.6, 2.1, calculate the value of the test statistic and clearly state your conclusion. Locate the value of the test statistic on your figure.
   3. What is the p-value of this test?

Answer 1

The sample size is n = 9 . The provided sample data along with the data required to compute the sample mean and sample variance are shown in the table below:

	X	X2
	0.9	0.81
	1.1	1.21
	0.1	0.01
	0.7	0.49
	0.4	0.16
	0.9	0.81
	0.8	0.64
	1.0	1
	0.4	0.16
Sum =	6.3	5.29

The sample mean is computed as follows:

Also, the sample variance  is

Therefore, the sample standard deviation s is

The sample size is n = 11. The provided sample data along with the data required to compute the sample mean and sample variance are shown in the table below:

	Y	Y2
	1.5	2.25
	0.9	0.81
	1.6	2.56
	0.5	0.25
	1.4	1.96
	1.9	3.61
	1.0	1
	1.2	1.44
	1.3	1.69
	1.6	2.56
	2.1	4.41
Sum =	15	22.54

The sample mean is computed as follows:

Also, the sample variance is

Therefore, the sample standard deviation s is

(1) Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

Ho: μ1​ = μ2​

Ha: μ1​ < μ2​

This corresponds to a left-tailed test, for which a t-test for two population means, with two independent samples, with unknown population standard deviations will be used.

(2) Rejection Region

Based on the information provided, the significance level is α=0.01, and the degrees of freedom are df = 18. In fact, the degrees of freedom are computed as follows, assuming that the population variances are equal:

Hence, it is found that the critical value for this left-tailed test is t_c = -2.552 , for α=0.01 and df = 18df=18.

(3) Test Statistics

Since it is assumed that the population variances are equal, the t-statistic is computed as follows:

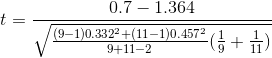
t = -3.637

(4) Decision about the null hypothesis

Since it is observed that t = -3.637 < t_c = -2.552, it is then concluded that the null hypothesis is rejected.

Using the P-value approach: The p-value is p = 0.0009, and since p = 0.0009 < 0.01p=0.0009<0.01, it is concluded that the null hypothesis is rejected.

(5) Conclusion

It is concluded that the null hypothesis Ho is rejected. Therefore, there is enough evidence to claim that population mean μ1​ is less than μ2​, at the 0.01 significance level.