Question

In 1995 ​, one county reported that among 3193 white women who had​ babies, 148 were multiple births. There were also 29 multiple births to 648 black women. Does this indicate any racial difference in the likelihood of multiple​ births? ​a) Test an appropriate hypothesis and state your conclusion. ​b) If your conclusion is​ incorrect, which type of error did you​ commit?

Answer 1

Solution:

Given:

white women:

n₁ = 3193

x₁ = Number of multiple births = 148

black women:

n₂= 648

x₂ = Number of multiple births = 29

Part a) Test an appropriate hypothesis and state your conclusion. ​

Step 1) State H0 and H1:

Vs

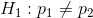
Step 2) Test statistic:

where

thus

Step 3) Find p-value:

p-value = 2 X P( Z > z) if z is positive.

p-value = 2 X P( Z < z) if z is negative

thus

p-value = 2 X P( Z > z)

p-value = 2 X P( Z > 0.18)

p-value = 2 X [ 1 - P( Z < 0.18) ]

Look in z table for z = 0.1 and 0.08 and find corresponding area.

P( Z<0.18) = 0.5714

thus

p-value = 2 X [ 1 - P( Z < 0.18) ]

p-value = 2 X [ 1 -0.5714 ]

p-value = 2 X 0.4286

p-value = 0.8572

Step 4) Decision Rule:
Reject null hypothesis H0, if P-value < 0.05 level of significance, otherwise we fail to reject H0

Since p-value = 0.8572 > 0.05 level of significance, we fail to reject H0

Step 5) Conclusion:

At 0.05 significance level,  this data does not indicate any racial difference in the likelihood of multiple​ births.

Part b) If your conclusion is​incorrect, which type of error did you​ commit?

Following are the definitions of Type 1 , Type 2 and correct decision.

Type 1 Error : Reject null hypothesis , in fact it is True.

Type 2 Error : Fail to reject null hypothesis , in fact it is False.

Correct decision: Reject H0, when it is False  or   Fail to reject H0, when it is True.

Since we failed to reject H0, and if this is incorrect then we have made Type 2 error.