Question
In: Physics
Consider a uniform density sphere of mass M and radius R in hydrostatic equilibrium with zero...
Consider a uniform density sphere of mass M and radius R in hydrostatic equilibrium with zero surface pressure. Derive expressions for the pressure P(r) and the gravitational potential phi(r) in terms of r, M, R, G and constants.
Solutions
Expert Solution
Let the uniform density be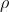 
.
Consider a thin shell of thickness dr at a distance r from the centre of the star. Mass of the shell dm will be,
Then the Gravitational force on the shell will be due to the interior mass of the star, Therfore we can write the gravitational force as.
The mass of the interior portion of the star can be written as,
Substituting we get,
This inward force is balanced by the outward pressure of the gas. The outward pressure will be
P(r) - P(r+dr) (Since P(r+dr) < P(r), The surface pressure is 0) (Here the sign followed is inward force is +ve, as in the case for gravitational force and outward force would be -ve)
Therfore we can write,
Now, we have to integrate both sides from R to distance r (since pressure at surface is 0), so as to find P(r)
Substituting value of density we can write,
Here, R is the radius of the star.
Gravitational potential is defined as work done per unit mass of the particle to bring a particle of mass m from infinity to the point at a distance of r, it can be evaluated by,
The gravitational potential for distance r>R is given by,
genius_generous answered 2 years agoRelated Solutions
Consider a thin uniform disk of mass M and radius R. A mass m is located...
Consider a thin uniform disk of mass M and radius R. A mass m is
located along the axis of the disk at a distance z from the center
of the disk. The gravitational force on the mass m (in terms of m,
M, R, G, and z) is
Consider a wire of uniform density and mass M shaped into a quarter circle of radius...
Consider a wire of uniform density and mass M shaped into a
quarter circle of radius R.The wire is located in the xy plane,
with the origin at the focus of the quarter circle (i.e at the
center of the circle of which the wire is part). Choose the x axis
parallel to the line that connects the endpoints of the wire, so
that the y-z plane is a plane of reflection symmetry for the wire.
This means that the...
A small solid sphere of mass M0, of radius R0, and of uniform density ρ0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ρ0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
Read it to me
R F U R or U F or U R or...
A small solid sphere of mass M0, of radius R0, and of uniform density ρ0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ρ0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
The new sphere has mass M = M0 and radius R >
R0
The new...
A small solid sphere of mass M0, of radius R0, and of uniform density ?0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ?0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
Read it to me
R F U R or U F or U R or...
A small solid sphere of mass M0, of radius R0, and of uniform density ρ0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ρ0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
The new sphere has mass M = M0 and density ρ <
ρ0
The new...
A small solid sphere of mass M0, of radius R0, and of uniform density ρ0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ρ0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
R F U R or U F or U R or F or U The new...
A small solid sphere of mass M0, of radius R0, and of uniform density ρ0 is...
A small solid sphere of mass M0, of radius
R0, and of uniform density ρ0 is placed in a
large bowl containing water. It floats and the level of the water
in the dish is L. Given the information below, determine the
possible effects on the water level L, (R-Rises, F-Falls,
U-Unchanged), when that sphere is replaced by a new solid sphere of
uniform density.
Read it to me
R F U R or U F or U R or...
A hollow sphere of mass M and radius R is hit by a pendulum of mass...
A hollow sphere of mass M and radius R is hit by a pendulum of
mass m and length L that is raised at an angle θ. After the
collision the pendulum comes to a stop and the sphere rolls forward
into a spring with stiffness k on an incline of ϕ. Find an
expression for how far ∆x the spring compresses along the incline.
Use only m, L, M, R, θ, ϕ, k and appropriate constants.
A non conducting sphere of radius R and uniform volume charge density is rotating with angular...
A non conducting sphere of radius R and uniform volume charge
density is rotating with angular velocity, Omega. Assuming the
center of the sphere is at the origin of the coordinate system, a)
what is the magnitude and direction of the resulting magnetic field
on the z axis for any arbitrary z distance away from the origin
when z > R? b) same question as part a) but for z < R? Omega
of the rotating sphere on the extra...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- Large lots are desirable in supply chain coordination despite increasing holding costs.
- ***Convert the C++ to Python*** #include <iostream> using std::cout; using std::cin; using std::endl; int charClass; char...
- Make-or-Buy Decision Fremont Computer Company has been purchasing carrying cases for its portable computers at a...
- The following costs were incurred for the single product produced during the first year of operations...
- Non-constant growth model: Do=$2.00 required return on equity= 5% g= 9% n=1,2 g=7% n=3,4 g=3% n=5...
- . Find all x ∈ Z143 such that x2Ξ 7 (mod 143). Please explain all steps...
- #Python: A palindrome is a sequence of characters that reads the same backwards as forwards. For...
ADVERTISEMENT