Question

A survey of the mean number of cents off that coupons give was conducted by randomly surveying one coupon per page from the coupon sections of a recent Rockford newspaper. The following data were collected: 20¢; 75¢; 50¢; 75¢; 30¢; 55¢; 10¢; 40¢; 30¢; 55¢; $1.50; 40¢; 65¢; 40¢. Assume the underlying distribution is approximately normal. Construct a 95% confidence interval for the population mean worth of coupons. Find the lower limit of the confidence interval. Enter it rounded to the nearest cent (2 decimal places)

Answer 1

Solution:

x	x2
20	400
75	5625
50	2500
75	5625
30	900
55	3025
10	100
40	1600
30	900
55	3025
1.5	2.25
40	1600
65	4225
40	1600
∑x=586.5	∑x2=31127.25

The sample mean is

Mean = (x / n) )

=20+75+50+75+30+55+10+40+30+55+1.5+40+65+40 /14

=586.5/14

=41.8929

Mean = 41.89

The sample standard is S

  S =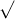( x2 ) - (( x)2 / n ) n -1

=√31127.25-(586.5)21413

=√31127.25-24570.1607/13

=√6557.0893/13

=√504.3915

=22.4587

Degrees of freedom = df = n - 1 = 14 - 1 = 13

At 95% confidence level the t is ,

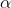  = 1 - 95% = 1 - 0.95 = 0.05

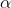/ 2 = 0.05 / 2 = 0.025

t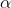 /2,df = t0.025,13 =2.160

Margin of error = E = t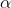/2,df * (s /n)

= 2.160 * (22.46 / 14)

= 12.97

Margin of error = 12.97

The 95% confidence interval estimate of the population mean is,

- E

41.89 - 12.97

= 28.92

The lower limit = 28.92