Question

1. Data were collected on number of credit hours earned from a random sample of 40 JMU students. The mean was 57.2 and the standard deviation was 8.9. Conduct a test to determine whether the true mean number of credit hours earned differs from 55.0, allowing a Type I error rate of 0.05. Assume that the distribution of the number of credit hours earned is normal. Show your full work. You may not use your calculator’s built-in function.

Answer 1

Solution:

The null and alternative hypothesis are

H0: = 55.0

H1:  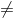   55.0

n = 40

= 57.2

s = 8.9

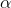= 0.05

Since population SD is unknown,we use t test.

The test statistics t is given by ..

t =  

= (57.2 - 55.0)/(8.9/40)

t = 1.563

n = 40

So , df = n - 1 = 40 - 1 = 39

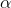= 0.05

So , 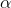/2  = 0.025

Now, 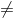sign in H1 indicates that the two tailed test.

So, the critical values are  

The critical region : t <   or t >  

  =   _0.025,39 = 2.023 (using t table)

t = 1.563 < 2.023

Fail to reject the null hypothesis.

There is no sufficient evidence to support the claim that  the true mean number of credit hours earned differs from 55.0.