Question

It is known that white sharks grow to a mean length of 18.9 feet.

A marine biologist claims that the great white sharks off the

coast of Bermuda grow much longer. Thirteen great white sharks

are captured, measured, and released off of Bermuda’s coast.

The mean length is 19.66 feet and the standard deviation is 2.6

feet. Does the data provide sufficient evidence at the .05 level

of significance to support the biologist’s claim?

Answer 1

Solution:

Given the hypothesis

H0: 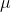= 18.9

H1: 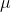> 18.9  

Use 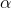  = 0.05 .... level of significance

Since population SD is unknown,we use t test.

The test statistics t is given by ..

t =  

= (19.66 - 18.9)/(2.6/13)

= 1.054

Test statistic t = 1.054

Here , n = 13 d.f. = n - 1 = 12

Now, >  sign in H1 indicates that the Right tailed test.(one tailed right sided )

So, the critical value is   i.e.  

The critical region : t >    

  =   _0.05,12 = 1.782 (using t table)

t = 1.054 <   

We Fail to reject the null hypothesis.

The data does not provide sufficient evidence at the .05 level of significance to support the biologist’s claim