Question

Michael measures the volume of several raindrops at Rainyville as 0.6 ml, 0.65 ml, 0.7 ml, 0.75 ml, 0.8 ml and 0.85 ml; and comes to believe that the raindrops at Rainyville are significantly larger than the national average of 0.65ml at the 5% level.

If Michael performs the appropriate statistical test, what will be his conclusion?

1. fail to reject the null hypothesis or 2. reject the null hypotheses

Answer 1

Solution

one sample t test for the the mean

Claim to be tested is   is larger than  the national average of 0.65ml

So hypothesis can be written as

H0: 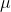= 0.65 ....null hypothesis

H1: 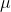> 0.65   ....alternative hypothesis

The sample of size n = 6 is taken.

0.6 ml, 0.65 ml, 0.7 ml, 0.75 ml, 0.8 ml and 0.85 ml

Let   and s be the sample mean and sample SD respectively.

=   

= (0.6 + 0.65+ ..........+ 0.85)/6

= 0.725

Now ,

s=   

Using given data, find Xi- for each term.take squre for each.then we can easily find s.

s= 0.09354143

The test statistic t is given by

t = ( - )/(s/n)

= (0.725 - 0.65)/(0.09354143/6)

= 1.964

Now , n = 6 implies d.f = n - 1 = 5

= 0.05 given

> sign in H1 indicates that the test is right tailed

So, the critical value is =   =  2.015 using t table.

So, t = 1.964 < = 2.015

So, we fail to reject the null hypothesis.