Question
In: Statistics and Probability
Statistics students in Oxnard College sampled 11 textbooks in the Condor bookstore and recorded the number...
Statistics students in Oxnard College sampled 11 textbooks in
the Condor bookstore and recorded the number of pages in each
textbook and its cost. The bivariate data are shown
below:
| Number of Pages (xx) | Cost(yy) |
|---|---|
| 446 | 60.9 |
| 909 | 134.35 |
| 430 | 67.5 |
| 628 | 93.2 |
| 475 | 67.25 |
| 504 | 69.6 |
| 875 | 140.25 |
| 296 | 41.4 |
| 214 | 45.1 |
| 884 | 135.6 |
| 655 | 106.25 |
A student calculates a linear model
y = x ___ + ____. (Please show your answers to two
decimal places)
Use the model to estimate the cost when number of pages is
547.
Cost = _____ $ (Please show your answer to 2 decimal places.)
Solutions
Expert Solution
Solution:
| X | Y | XY | X2 | Y2 | |
| 446 | 60.9 | 27161.4 | 198916 | 3708.81 | |
| 909 | 134.35 | 122124.2 | 826281 | 18049.9225 | |
| 430 | 67.5 | 29025 | 184900 | 4556.25 | |
| 628 | 93.2 | 58529.6 | 394384 | 8686.24 | |
| 475 | 67.25 | 31943.75 | 225625 | 4522.5625 | |
| 504 | 69.6 | 35078.4 | 254016 | 4844.16 | |
| 875 | 140.25 | 122718.8 | 765625 | 19670.0625 | |
| 296 | 41.4 | 12254.4 | 87616 | 1713.96 | |
| 214 | 45.1 | 9651.4 | 45796 | 2034.01 | |
| 884 | 135.6 | 119870.4 | 781456 | 18387.36 | |
| 655 | 106.25 | 69593.75 | 429025 | 11289.0625 | |
n = 11
Slope of the regression line is
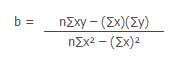
b = 0.15
Now , y intercept of the line is
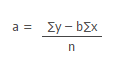
a = 0.3955 = 0.40
The equation of the regression line is
= bx + a
y = 0.15 x + 0.40
Now ,
For x = 547 , find the predicted value of y .
Put x = 547 in the regression line equation.
= (0.15*547) + 0.40 = 82.45
Cost = 82.45 $
orchestra answered 1 year agoRelated Solutions
Statistics students in Oxnard College sampled 11 textbooks in the Condor bookstore and recorded the number...
Statistics students in Oxnard College sampled 11 textbooks in
the Condor bookstore and recorded the number of pages in each
textbook and its cost. The bivariate data are shown
below:
Number of Pages (xx)
Cost(yy)
761
66.27
855
57.85
681
60.67
658
42.06
218
24.26
587
44.09
973
72.11
925
68.75
672
45.04
426
28.82
243
28.01
A student calculates a linear model
yy = xx + . (Please show your answers to two decimal
places)
Use the model to estimate...
22 Statistics students in Oxnard College sampled 11 textbooks in the Condor bookstore, and recorded number...
22
Statistics students in Oxnard College sampled 11 textbooks in
the Condor bookstore, and recorded number of pages in each textbook
and its cost. The bivariate data is shown below,
Number of Pages (xx)
Cost(yy)
513
65.43
323
34.53
751
87.61
619
70.09
671
80.81
914
101.54
310
44.1
321
51.31
243
45.73
496
63.56
528
59.08
A student calculates a linear model
yy = xx + . (Please show your answers to two decimal
places)
Use the model above to...
Statistics students in Oxnard College sampled 9 textbooks in the Condor bookstore and recorded the number...
Statistics students in Oxnard College sampled 9 textbooks in the
Condor bookstore and recorded the number of pages in each textbook
and its cost. The bivariate data are shown below:
Number of Pages (xx)
Cost(yy)
470
65.4
980
135.6
300
53
888
117.56
982
128.84
762
110.44
267
41.04
571
88.52
640
91.8
A student calculates a linear model
yy = xx + . (Please show your answers to two decimal
places)
Use the model to estimate the cost when number...
Statistics students in Oxnard College sampled 10 textbooks in the Condor bookstore, and recorded number of...
Statistics students in Oxnard College sampled 10 textbooks in
the Condor bookstore, and recorded number of pages in each textbook
and its cost. The bivariate data is shown below,
Number of Pages (xx)
Cost(yy)
526
52.08
625
59
589
56.12
409
25.72
489
34.12
500
53
906
78.48
251
26.08
595
50.6
719
68.52
A student calculates a linear model
yy = xx + . (Please show your answers to two decimal
places)
Use the model above to estimate the cost...
The college bookstore tells prospective students that the average cost of its textbooks is $52 with...
The college bookstore tells prospective students that the
average cost of its textbooks is $52 with a σ of $4.50. A group of
smart statistics students think that the average cost is much
higher. In order to test the bookstore’s claim against their
alternative, the students select a random sample of size 100.
Assume that the mean from their random sample is $52.80. Use alpha
value of 0.05 level to test the hypothesis.
The college bookstore tells prospective students that the average cost of its textbooks is $52 with...
The college bookstore tells prospective students that the
average cost of its textbooks is $52 with a standard deviation of
$4.50. A group of smart statistics students thinks that the average
cost is higher. In order to test the bookstore’s claim against
their alternative, the students will select a random sample of size
100. Assume that the mean from their random sample is $52.80. Test
at 10% significance level.
--> Perform a hypothesis test and state your decision.
The college bookstore tells prospective students that the average cost of its textbooks is $108 with...
The college bookstore tells prospective students that the
average cost of its textbooks is $108 with a standard deviation of
$4.50. A group of smart statistics students thinks that the average
cost is higher. In order to test the bookstore’s claim against
their alternative, the students will select a random sample of size
100. Assume that the mean from their random sample is $112.80.
Perform a hypothesis test (using R) at the 5% level of
significance and state your decision....
6. The college bookstore tells prospective students that the average cost of its textbooks is $42...
6. The college bookstore tells prospective students that the
average cost of its textbooks is $42 with a standard deviation of
$2.50. A group of smart statistics students thinks that the average
cost is higher. In order to test the bookstore’s claim against
their alternative, the students will select a random sample of size
100. Assume that the mean from their random sample is $42.80.
Perform a hypothesis test at the 5% level of significance and state
your decision
In our Condor Cafe, the Oxnard College Culinary Program offers the most delicious and affortable breakfast...
In our Condor Cafe, the Oxnard College Culinary Program offers
the most delicious and affortable breakfast and lunch choices among
the 152 Community Colleges in California. This week, a random
sample of 386 orders were recorded, and 242 orders were for the
$5-meals. Please find the 99% confidence interval for the true
proportion of the orders for the $5-meals. Enter your answer as an
open-interval (i.e., parentheses) using decimals (not percents)
accurate to three decimal places. Confidence interval = Express...
In our Condor Cafe, the Oxnard College Culinary Program offers the most delicious and affortable breakfast...
In our Condor Cafe, the Oxnard College Culinary Program offers
the most delicious and affortable breakfast and lunch choices among
the 152 Community Colleges in California. This week, a random
sample of 186 orders were recorded, and 57 orders were for the
$5-meals. Please find the 99.9% confidence interval for the true
proportion of the orders for the $5-meals.
A. Enter your answer as an open-interval
(i.e., parentheses) using decimals (not percents) accurate
to three decimal places.
Confidence interval =...
ADVERTISEMENT
ADVERTISEMENT
Latest Questions
- b. Do any unions represent employees in Microsoft? Describe which unions are involved. c. Have there been...
- Look up and use each of these Linux commands. (Each command will have two parts) Summarize...
- What was Lincoln 10 percent plan and what problems did it present?
- A cantilever beam 4m long carries a uniform load of 3.5 kN/m over a portion 1.5m...
- Our next optimization comes from using the brilliant Rabin-Karp substring matching algorithm (RK for short), invented...
- Give an example of an experiment to determine the focal length of a concave lens. (Note...
- Search the Internet to find (at least 2 websites) related to the general field of malware....
ADVERTISEMENT