Question

A soda vending machine is supposed to dispense 7 fluid ounces of soda into a cup. The canteen manager tested the machine by taking a sample of 20 cups of soda. He measured the 20 cups of soda individually and found that the measurements had a mean of 8.08 fl. oz. and a standard deviation of 2.85 fl. oz. Determine if the machine dispense is different from the required ounces set by the company.

(a) State the null hypothesis and alternative hypothesis

(b) Find the test statistic

(c) If the type-I error α = 0.1, find the critical value(s) and shade the rejection region(s)

(d) Base on the type-I error α and rejection region(s), given above, what is your conclusion?

Answer 1

Solution:

a)

H0: 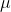= 7

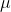
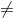H1:     7

b)

The test statistics t is given by ..

t =  

= (8.08 - 7)/(2.85/20)

= 1.695

Test statistic t = 1.695

c)

= 0.1

/2 = 0.05

n = 20

df = n - 1 = 20 - 1 = 19

Now, 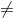sign in H1 indicates that the two tailed test.

So, the critical values are   i.e.   =   =   1.729

Critical values are -1.729 , 1.729

rejection regions : t < -1.729 OR t > 1.729

d)

Decision: Do not reject H0

(Because test statistic t = 1.695 is not in the rejection region.

Conclusion: There is no sufficient evidence to support that  the machine dispense is different from the required ounces set by the company.