Question

 

Learning Goal: To understand the continuity equation.

Streamlines represent the path of the flow of a fluid. You can imagine that they represent a time-exposure photograph that shows the paths of small particles carried by the flowing fluid. The figure shows streamlines for the flow of an incompressible fluid in a tapered pipe of circular cross section. The speed of the fluid as it enters the pipe on the left is v₁. Assume that the cross-sectional areas of the pipe are A₁ at its entrance on the left and A₂ at its exit on the right.

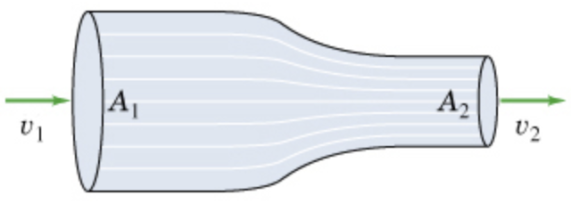
Part A

Find F₁, the volume of fluid flowing into the pipe per unit of time. This quantity is also known as the volumetric flow rate.

Express the volumetric flow rate in terms of any of the quantities given in the problem introduction.

 

Part B

Because the fluid is assumed to be incompressible and mass is conserved, at a particular moment in time, the amount of fluid that flows into the pipe must equal the amount of fluid that flows out. This fact is embodied in the continuity equation. Using the continuity equation, find the velocity v₂ of the fluid flowing out of the right end of the pipe.

Express your answer in terms of any of the quantities given in the problem introduction.

 

 

Part C

If you are shown a picture of streamlines in a flowing fluid, you can conclude that the __________ of the fluid is greater where the streamlines are closer together.

Enter a one-word answer.

 

Answer 1

Concepts and reason

The concept required to solve this problem is the continuity equation. Initially, find the volume of fluid which is entering in the pipe and then find the length of the region from where the fluid has entered the pipe in time interval \(\Delta t\). Then, find the volumetric flow rate. Later, find the volumetric flow rate flowing out of the pipe. Then, use the continuity equation to find the velocity of the fluid flowing out of the pipe. Finally, find which quantity increases with the increase in the density of the streamlines.

Fundamentals

The expression of the volume is, \(V=A L\)

Here, \(\mathrm{V}\) is the volume, \(\mathrm{A}\) is the area, and \(\mathrm{L}\) is the length. The expression of the speed is, \(v=\frac{L}{t}\)

Here, v is the speed, Lis the distance, and \(t\) is the time. The expression of the continuity equation is, \(A_{1} v_{1}=A_{2} v_{2}\)

Here, \(A_{1}\) is the area of the pipe through which the fluid is entering, \(v_{1}\) is the speed of the fluid entering the pipe, \(A_{2}\) is the area of the pipe from where the fluid is flowing out, and \(v_{2}\) is the speed of the fluid through which it is going outside the pipe.

 

(A) The expression of the volume of fluid which is entering in the pipe using the area and the length of the region covered by the fluid in time \(\Delta t\) is, \(\Delta V=A_{1} L_{1}\)

The length of the region from where the fluid has entered the pipe in time interval \(\Delta t\) is, \(L_{1}=v_{1} \Delta t\)

Substitute \(v_{1} \Delta t\) for \(L_{1}\) in the expression of the volume \(\Delta V\) \(\Delta V=A_{1} v_{1} \Delta t\)

Rearrange the equation for volumetric flow rate. \(\frac{\Delta V}{\Delta t}=A_{1} v_{1}\)

Substitute \(F_{1}\) for \(\frac{\Delta V}{\Delta t}\) \(F_{1}=A_{1} v_{1}\)

Part A

The volumetric flow rate is \(F_{1}=A_{1} v_{1}\)

The volumetric flow rate can be defined as the volume of a fluid flowing per unit time. The length of the region from where the fluid has entered the pipe in time interval \(\Delta t\) is equal to the speed of the fluid entering in the pipe multiplied by time.

 

(B) The mass is conserved. The expression of mass in terms of density is, \(m=\rho V\)

Here, \(\mathrm{m}\) is the mass, \(\rho\) is the density, and \(\mathrm{V}\) is the volume. Divide the expression by the time interval t. \(\frac{m}{t}=\rho \frac{V}{t}\)

The flow rate is, \(F_{1}=F_{2}\)

The volumetric flow \(F_{2}\) out of the pipe per unit time is, \(F_{2}=A_{2} v_{2}\)

Here, \(A_{2}\) is the area of the pipe when the fluid id flowing out with the speed \(v_{2}\). Use continuity equation. \(A_{1} v_{1}=A_{2} v_{2}\)

Rearrange for \(v_{2}\). \(v_{2}=\frac{A_{1} v_{1}}{A_{2}}\)

Part B The velocity \(v_{2}\) of the fluid flowing out of the right end of the pipe is \(v_{2}=\frac{A_{1} v_{1}}{A_{2}}\).

The continuity equation states that the volumetric flow into the pipe and out of the pipe should be same. The velocity \(v_{2}\) of the fluid flowing out of the right end of the pipe can be written in terms of the area of the pipe through which the fluid is entering the pipe with the velocity \(v_{1}\) and the area \(A_{2}\) of the pipe through which the fluid is flowing out.

 

(C) The streamline flow implies that the flow of fluid in which the speed at any point is constant. The closer the streamline implies the increasing density of streamlines which leads to the increase in the velocity of the fluid. The velocity of the flow will increase with the increase of the density of streamlines.

Part \(C\) Velocity.

If the picture of a streamline is shown, it can be concluded that the velocity of the fluid is greater where the streamlines are closer together. The velocity of the flow will increase with the increase of the density of streamlines.

 

Part A The volumetric flow rate is \(F_{1}=A_{1} v_{1}\)

Part B The velocity \(v_{2}\) of the fluid flowing out of the right end of the pipe is \(v_{2}=\frac{A_{1} v_{1}}{A_{2}} .\)

Part \(C\) Velocity.