Question

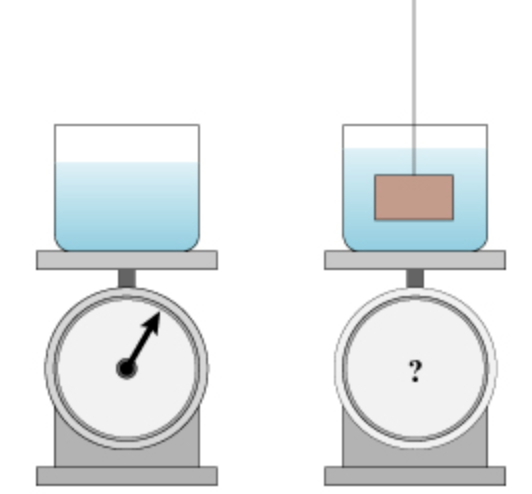
A flask of water rests on a scale that reads 100 N. Then, a small block of unknown material is held completely submerged in the water. The block does not touch any part of the flask, and the person holding the block will not tell you whether the block is being pulled up (keeping it from falling further) or pushed down (keeping it from bobbing back up).

The experiment is repeated with the six different blocks listed below. In each case, the blocks are held completely submerged in the water.

Mass (g)	Volume (cm3)
A	100	50
B	100	200
C	200	50
D	50	100
E	200	100
F	400	50

 

Part B

Rank these blocks on the basis of the scale reading when the blocks are completely submerged.

Rank from largest to smallest. To rank items as equivalent, overlap them.

 

Part C

If the blocks were released while submerged, which, if any, would sink to the bottom of the flask?

Enter the correct letters from the table in alphabetical order without commas or spaces (e.g., ABC).

 

 

Answer 1

 

Concepts and reason

The concepts used to solve this problem are buoyancy and Archimedes principle. Use the relation between the buoyant force and volume to rank the blocks based on scale reading when they are completely submerged. Use the density to rank the blocks that released while submerged would sink at the flask's bottom.

Fundamentals

When a block is completely immersed in water, two vertical forces act upon the block. The downward forces acting on the block are the block's weight and downward thrust due to the pressure of the liquid on the upper surface of the block. The upwards forces acting on the block are the spring tension, which measures the apparent weight and the upward thrust due to the liquid present below the lower surface of the block. This upward thrust is called buoyancy. The following diagram shows the free body diagram of gravity and thrust.

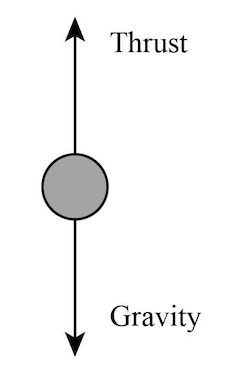
When the object is completely immersed in the water, the loss in weight of the body increases. Archimedes Principle states that when an object is immersed in a liquid, an upward thrust, equal to the liquid displaced's weight, acts on it. Thus when a block is completely immersed in a liquid, it loses weight, equal to the weight of the liquid it displaces. \(B=W\)

Here, \(B\) is the buoyant force, and \(W\) is the weight of the liquid displaced. The expression for the buoyant force is, \(B=\rho V g\)

Here, \(\rho\) is the density of the liquid, \(V\) is the volume of the liquid displaced, and \(g\) is the acceleration due to gravity. The expression for the density is,

\(\rho=\frac{m}{V}\)

Here, \(\mathrm{m}\) is the mass, and \(\mathrm{V}\) is the volume.

 

(B) 

The buoyant force of Block A is,

\(B_{A}=\rho V_{A} g\)

Here, \(B_{A}\) is the buoyant force of block \(A, g\) is the acceleration due to gravity, and \(V_{A}\) is the volume of the block \(A\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g,\) and \(50 \mathrm{~cm}^{3}\) for \(V_{A}\)

$$ \begin{aligned} B_{A} &=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(50 \mathrm{~cm}^{3}\right) \\ &=5 \mathrm{~N} \end{aligned} $$

Buoyant force of Block \(\mathrm{B}\) is,

\(B_{B}=\rho V_{B} g\)

Here, \(B_{B}\) is the buoyant force of block \(B\) and \(V_{B}\) is the volume of the block \(B\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\), and \(200 \mathrm{~cm}^{3}\) for \(V_{B}\)

$$ \begin{aligned} B_{B} &=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(200 \mathrm{~cm}^{3}\right) \\ &=20 \mathrm{~N} \end{aligned} $$

Buoyant force of Block \(C\) is,

\(B_{C}=\rho V_{C} g\)

Here, \(B_{C}\) is the buoyant force of block \(C\) and \(V_{C}\) is the volume of the block \(C\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\), and \(50 \mathrm{~cm}^{3}\) for \(V_{C}\).

$$ \begin{aligned} B_{C} &=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(50 \mathrm{~cm}^{3}\right) \\ &=5 \mathrm{~N} \end{aligned} $$

Buoyant force of Block D is,

\(B_{D}=\rho V_{D} g\)

Here, \(B_{D}\) is the buoyant force of block \(D\) and \(V_{D}\) is the volume of the block \(D\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g\), and \(100 \mathrm{~cm}^{3}\) for \(V_{D}\).

$$ \begin{aligned} B_{D} &=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(100 \mathrm{~cm}^{3}\right) \\ &=10 \mathrm{~N} \end{aligned} $$

Buoyant force of Block \(\mathrm{E}\) is,

$$ B_{E}=\rho V_{E} g $$

Here, \(B_{E}\) is the buoyant force of block \(E\) and \(V_{E}\) is the volume of the block \(E\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g,\) and \(100 \mathrm{~cm}^{3}\) for \(V_{E}\)

$$ B_{E}=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(100 \mathrm{~cm}^{3}\right) $$

\(=10 \mathrm{~N}\)

Buoyant force of Block \(\mathrm{F}\) is,

\(B_{F}=\rho V_{F} g\)

Here, \(B_{F}\) is the buoyant force of block \(\mathrm{F}\) and \(V_{F}\) is the volume of the block \(\mathrm{F}\).

Substitute \(10 \mathrm{~g} / \mathrm{cm}^{3}\) for \(\rho, 10 \mathrm{~m} / \mathrm{s}^{2}\) for \(g,\) and \(50 \mathrm{~cm}^{3}\) for \(V_{E}\)

$$ B_{E}=\left(10\left(\frac{\mathrm{g}}{\mathrm{cm}^{3}}\right)\left(\frac{1 \mathrm{~kg}}{1000 \mathrm{~g}}\right)\right)\left(10 \mathrm{~m} / \mathrm{s}^{2}\right)\left(50 \mathrm{~cm}^{3}\right) $$

\(=5 \mathrm{~N}\)

Part B Blocks are ranked largest to smallest on the basis of scale reading when the blocks are completely submerged

are \(B_{B}>\left(B_{D}=B_{E}\right)>\left(B_{A}=B_{C}=B_{F}\right)\)

Immersion of the object in the liquid depends on the density and the volume of the liquid. The buoyant force exerted on an object by a liquid is proportional to the volume of the liquid displaced by that object. Volume of liquid displaced is equal to the upward force which reflects the weight of the object submerged into the liquid. Thus the mass is negligible here and from the given data volume is to be considered. Hence larger volume block is completely submerged into the water.

 

(C) 

Expression for the density of the block A is,

\(\rho_{A}=\frac{m_{A}}{V_{A}}\)

Here, \(\rho_{A}\) is the density of the block \(\mathrm{A}, m_{A}\) is the mass of the block \(\mathrm{A}\), and \(V_{A}\) is the volume of the block \(\mathrm{A}\).

Substitute \(100 \mathrm{~g}\) for \(m_{A}\) and \(50 \mathrm{~cm}^{3}\) for \(V_{A}\)

\(\rho_{A}=\frac{(100 \mathrm{~g})}{\left(50 \mathrm{~cm}^{3}\right)}\)

\(=2 \mathrm{~g} / \mathrm{cm}^{3}\)

Expression for the density of the block \(\mathrm{B}\) is,

\(\rho_{B}=\frac{m_{B}}{V_{B}}\)

Here, \(\rho_{B}\) is the density of the block \(\mathrm{B}, m_{B}\) is the mass of the block \(\mathrm{B}\), and \(V_{B}\) is the volume of the block \(\mathrm{B}\).

Substitute \(100 \mathrm{~g}\) for \(m_{B}\) and \(200 \mathrm{~cm}^{3}\) for \(V_{B}\)

\(\rho_{B}=\frac{(100 \mathrm{~g})}{\left(200 \mathrm{~cm}^{3}\right)}\)

\(=0.5 \mathrm{~g} / \mathrm{cm}^{3}\)

Expression for the density of the block \(C\) is,

\(\rho_{C}=\frac{m_{C}}{V_{C}}\)

Here, \(\rho_{C}\) is the density of the block \(C, m_{C}\) is the mass of the block \(C\), and \(V_{C}\) is the volume of the block \(C\).

Substitute \(200 \mathrm{~g}\) for \(m_{C}\) and \(50 \mathrm{~cm}^{3}\) for \(V_{C}\)

\(\rho_{C}=\frac{(200 \mathrm{~g})}{\left(50 \mathrm{~cm}^{3}\right)}\)

\(=4 \mathrm{~g} / \mathrm{cm}^{3}\)

Expression for the density of the block \(D\) is,

\(\rho_{D}=\frac{m_{D}}{V_{D}}\)

Here, \(\rho_{D}\) is the density of the block \(D, m_{D}\) is the mass of the block \(D\), and \(V_{D}\) is the volume of the block \(D\).

Substitute \(50 \mathrm{~g}\) for \(m_{D}\) and \(100 \mathrm{~cm}^{3}\) for \(V_{D}\)

\(\rho_{D}=\frac{(50 \mathrm{~g})}{\left(100 \mathrm{~cm}^{3}\right)}\)

\(=0.5 \mathrm{~g} / \mathrm{cm}^{3}\)

Expression for the density of the block \(\mathrm{E}\) is,

\(\rho_{E}=\frac{m_{E}}{V_{E}}\)

Here, \(\rho_{E}\) is the density of the block \(\mathrm{E}, m_{E}\) is the mass of the block \(\mathrm{E}\), and \(V_{E}\) is the volume of the block \(\mathrm{E}\).

Substitute \(200 \mathrm{~g}\) for \(m_{E}\) and \(100 \mathrm{~cm}^{3}\) for \(V_{E}\)

\(\rho_{E}=\frac{(200 \mathrm{~g})}{\left(100 \mathrm{~cm}^{3}\right)}\)

\(=2 \mathrm{~g} / \mathrm{cm}^{3}\)

Expression for the density of the block \(\mathrm{F}\) is,

\(\rho_{F}=\frac{m_{F}}{V_{F}}\)

Here, \(\rho_{F}\) is the density of the block \(\mathrm{F}, m_{F}\) is the mass of the block \(\mathrm{F}\), and \(V_{F}\) is the volume of the block \(\mathrm{F}\).

Substitute \(400 \mathrm{~g}\) for \(m_{F}\) and \(50 \mathrm{~cm}^{3}\) for \(V_{F}\)

\(\rho_{F}=\frac{(400 \mathrm{~g})}{\left(50 \mathrm{~cm}^{3}\right)}\)

\(=8 \mathrm{~g} / \mathrm{cm}^{3}\)

Part \(C\) 

If the blocks were released while submerged, blocks ACEF will sink to the bottom of the flask.

The density of water is \(1 \mathrm{~g} / \mathrm{cm}^{3}\). Only blocks of lesser or equal to the density of the water can float in water. Blocks of greater density than the density of water will sink to the bottom of the flask.

Part B

Blocks are ranked largest to smallest on the basis of scale reading when the blocks are completely submerged are

\(B_{B}>\left(B_{D}=B_{E}\right)>\left(B_{A}=B_{C}=B_{F}\right)\)

Part C

If the blocks were released while submerged, blocks ACEF will sink to the bottom of the flask.