Question

Find the regression​ equation, letting the first variable be the predictor​ (x) variable. Using the listed​ lemon/crash data, where lemon imports are in metric tons and the fatality rates are per​ 100,000 people, find the best predicted crash fatality rate for a year in which there are 475 metric tons of lemon imports. Is the prediction​ worthwhile?

Lemon Imports 235 270 359 500 533

Crash Fatality Rate 16.1 16 15.8 15.6 15.12

Answer 1

Solution:

From given data , we prepare a table.

X	Y	XY	X^2	Y^2
235	16.1	3783.5	55225	259.21
270	16	4320	72900	256
359	15.8	5672.2	128881	249.64
500	15.6	7800	250000	243.36
533	15.12	8058.96	284089	228.6144

n	5
sum(XY)	29634.66
sum(X)	1897.00
sum(Y)	78.62
sum(X^2)	791095.00
sum(Y^2)	1236.82
b	-0.0027
a	16.7540

Now ,

Slope of the regression line is

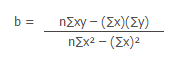
   b = - 0.0027

Now , y intercept of the line is

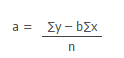
   a = 16.7540

The equation of the regression line is

= a + bx

i.e. = 16.7540 + (-0.0027)X

For x = 475 , find the predicted value of y .

Put x = 475 in the regression line equation.

= a + bx

= 16.7540 + ( - 0.0072 * 475)

Answer: y = 45.4715