Consider the slope field shown. (a) For the solution that satisfies y(0) = 0, sketch the solution curve and estimate the following

Consider the slope field shown.

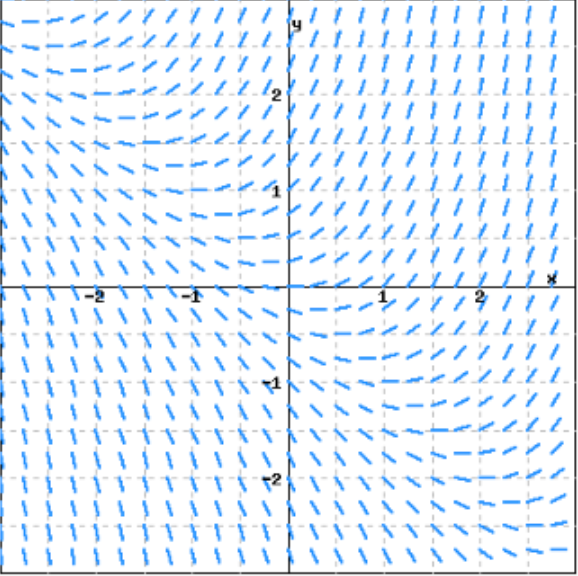
(a) For the solution that satisfies y(0) = 0, sketch the solution curve and estimate the following:

y(1) ≈ _______ and y(-1) ≈ _______

(b) For the solution that satisfies y(0) = 1, sketch the solution curve and estimate the following:

y(0.5) ≈ _______ and y(-1) ≈ _______

(c) For the solution that satisfies y(0) = -1, sketch the solution curve and estimate the following:

y(1) ≈ _______ and y(-1) ≈ _______

Expert Solution

ANSWER:
a) Solution curve with y(0)- 0 is given below In this case, we havel)0.5, y-1)0.5 b) Solution curve through yf0)- isgven below ะ 1.5, y(-1)~0.75 Based on this, we can say that y(0.5) c Solution curve passing through y(0) s gven below: Based on this curve, we can say that y(1)~-2, y(-1)~0

milcah answered 2 years ago

y'' + 16y = (8)(cos(4t)) y(0)=y'(0)= 0 Use Laplace Transforms to solve. Sketch the solution or...

y'' + 16y = (8)(cos(4t)) y(0)=y'(0)= 0 Use Laplace Transforms to solve. Sketch the solution or use matlab to show the graph.

At a relative maximum of a curve y(x), the slope dy/dx is zero. Use the following data to estimate the values of x and y that co

At a relative maximum of a curve y(x), the slope dy/dx is zero. Use the following data to estimate the values of x and y that correspond to a maximum point.

Consider the system x'= -y , y' = -x Sketch the vector field using math-lab. Please...

Consider the system x'= -y , y' = -x Sketch the vector field using math-lab. Please write the code with all the steps. I'm new on math-lab, and I tried to follow some online videos but it did not work right. I have the sketch, but I need the code and the steps to learn it. Thank you,

Sketch the graph of the curve ? = 1 + sin ? for 0 ≤ ?...

Sketch the graph of the curve ? = 1 + sin ? for 0 ≤ ? ≤ 2? ? b) Find the slope of the tangent line to this curve at ? = 4 . c) Find the polar coordinates of the points on this curve where the tangent line is horizontal.

Consider the following initial value problem. y''−4y = 0, y(0) = 0, y'(0) = 5 (a)...

Consider the following initial value problem. y''−4y = 0, y(0) = 0, y'(0) = 5 (a) Solve the IVP using the characteristic equation method from chapter 4. (b) Solve the IVP using the Laplace transform method from chapter 7. (Hint: If you don’t have the same ﬁnal answer for each part, you’ve done something wrong.)

Consider a function f(x) which satisfies the following properties: 1. f(x+y)=f(x) * f(y) 2. f(0) does...

Consider a function f(x) which satisfies the following properties: 1. f(x+y)=f(x) * f(y) 2. f(0) does not equal to 0 3. f'(0)=1 Then: a) Show that f(0)=1. (Hint: use the fact that 0+0=0) b) Show that f(x) does not equal to 0 for all x. (Hint: use y= -x with conditions (1) and (2) above.) c) Use the definition of the derivative to show that f'(x)=f(x) for all real numbers x d) let g(x) satisfy properties (1)-(3) above and let...

(a) On a separate sheet of paper, sketch the parameterized curve x=tcost, y=tsint for 0≤t≤4π. Use...

(a) On a separate sheet of paper, sketch the parameterized curve x=tcost, y=tsint for 0≤t≤4π. Use your graph to complete the following statement: At t=6t=6, a particle moving along the curve in the direction of increasing t is moving _________ and _____________ (b) By calculating the position at t=6 and t=6.01, estimate the speed at t=6. speed ≈___________ (c) Use derivatives to calculate the speed at t=6 and compare your answer to part (b). speed ≈___________

Consider the solution of the differential equation y′=−3yy′=−3y passing through y(0)=0.5y(0)=0.5.

Consider the solution of the differential equation y′=−3yy′=−3y passing through y(0)=0.5y(0)=0.5. A. Sketch the slope field for this differential equation, and sketch the solution passing through the point (0,0.5). B. Use Euler's method with step size Δx=0.2Δx=0.2 to estimate the solution at x=0.2,0.4,…,1x=0.2,0.4,…,1, using these to fill in the following table. (Be sure not to round your answers at each step!) x=x= 0 0.2 0.4 0.6 0.8 1.0 y≈y≈ 0.5 C. Plot your estimated solution...

Find the general solution and solve the IVP y''+y'-y=0, y(0)=2, y'(0)=0

1. (a) Sketch the slope field for the given differential equation: dy/dx = 2? (b) Find...

1. (a) Sketch the slope field for the given differential equation: dy/dx = 2? (b) Find the particular solution of the differential equation that satisfies the initial condition y(0) = 4 (c) What is the value of y when x = 1/2 2. (a) Find the general solution of the given differential equation: dy/dx = ysinx = ????? 2 (b) Find the particular solution of the differential equation that satisfies the initial condition ? = 2; ?ℎ?? ? = π/2

Question