Question
In: Math
Consider the following sample data. Sample A: 10, 17, 24 Sample B: 68, 75, 82 Sample...
Consider the following sample data.
| Sample A: | 10, 17, 24 |
| Sample B: | 68, 75, 82 |
| Sample C: | 1,035; 1,042; 1,049 |
(a) Find the mean and standard deviation for each
sample.
| Sample A: | Sample B: | Sample C: | |
| Mean | |||
| Sample Standard Deviation | |||
(b) What does this exercise show about the
standard deviation?
____The idea is to illustrate that the standard deviation is not a function of the value of the mean.
____The idea is to illustrate that the standard deviation is a function of the value of the mean.
Solutions
Expert Solution
GIVEN:
| Sample A | 10, 17, 24 |
| Sample B | 68, 75, 82 |
| Sample C | 1035, 1042, 1049 |
SOLUTION:
MEAN AND STANDARD DEVIATION OF SAMPLE A:
The mean for sample A is given by,

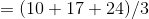
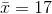
The standard deviation for sample A is given by,
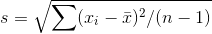
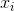 |
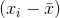 |
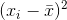 |
| 10 | -7 | 49 |
| 17 | 0 | 0 |
| 24 | 7 | 49 |
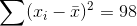 |
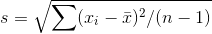
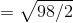
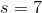
The mean for sample A is
 .
.
The standard deviation for
sample A is  .
.
MEAN AND STANDARD DEVIATION OF SAMPLE B:
The mean for sample B is given by,

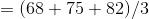
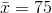
The standard deviation for sample B is given by,
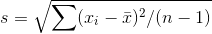
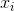 |
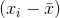 |
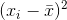 |
| 68 | -7 | 49 |
| 75 | 0 | 0 |
| 82 | 7 | 49 |
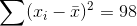 |
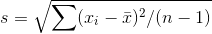
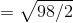
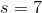
The mean for sample B is
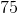 .
.
The standard deviation for
sample B is 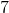 .
.
MEAN AND STANDARD DEVIATION OF SAMPLE C:
The mean for sample C is given by,

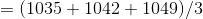
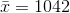
The standard deviation for sample C is given by,
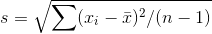
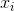 |
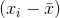 |
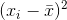 |
| 1035 | -7 | 49 |
| 1042 | 0 | 0 |
| 1049 | 7 | 49 |
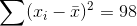 |
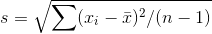
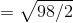
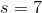
The mean for sample C is
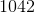 .
.
The standard deviation for
sample C is 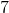 .
.
(b) What does this exercise show about the standard deviation?
Standard deviation measures the spread or dispersion of a data distribution. The variability of data points around the mean is same for all three samples given. The idea is to illustrate that the standard deviation is a function of the value of the mean.
Related Solutions
Consider the following sample. 17, 7, 25, 20, 10, 18 (a) Find the range. (b) Find...
Consider the following set of data. (18, 15), (31, 55), (63, 27), (82, 24), (109, 58),...
Consider the data. xi 2 6 9 13 20 yi 7 17 10 28 24 (a)...
For the following data 86 84 91 75 78 80 74 75 87 76 82 90...
A sample of size 82 will be drawn from a population with mean 24 and standard...
Consider a sample with data values of 27, 24, 22, 15, 31, 33, 28, and 24....
Consider a sample with data values of 27, 24, 22, 16, 30, 35, 29, and 24....
Consider a sample with data values of 26, 24, 23, 18, 31, 35, 29, and 24....
Consider the following sample data. Sample A: 14, 16, 18 Sample B: 72, 74, 76 Sample...
Consider the following sample data. Sample A: 4, 6, 8 Sample B: 63, 65, 67 Sample...
- (python only) Assignment: Guess a number To get started, open IDLE and create a New File...
- cpp program to read a triangle three sides and print" equilateral" when all the sides are...
- 1. Explain, with the use of examples, when it would be appropriate to use trademarks and...
- A new golf ball design is being evaluated. A random sample of 100 pro golfers and...
- This week, we are focusing on Management and Motivation (Chapter 3). Be sure to read chapter...
- A 2.00 m long horizontal uniform beam is supported by a wire as shown in the...
- State two reasons why it is advisable to place the transaction log on a separate disk...
 milcah answered 3 weeks ago
milcah answered 3 weeks ago