Question

An employee of a small software company in Minneapolis bikes to work during the summer months. He can travel to work using one of three routes and wonders whether the average commute times (in minutes) differ between the three routes. He obtains the following data after traveling each route for one week.

Route	Minutes
Route 1	27
Route 1	34
Route 1	25
Route 1	31
Route 1	28
Route 2	25
Route 2	25
Route 2	26
Route 2	25
Route 2	26
Route 3	29
Route 3	20
Route 3	26
Route 3	21
Route 3	21

ANOVA
Source of Variation	Df	Sum Sq	Mean Sq	F value	Pr(>F)
Section
Residuals

Use Tukey’s HSD method at the 5% significance level to determine which routes' average times differ. (Round difference to 1 decimal place, confidence interval bounds to 2 decimal places, and p-values to 3.)

Population Mean Difference	diff	lwr	upr	p adj	Do the average times differ?
Route 2 - Route 1
Route 3 - Route 1
Route 3 - Route 2

Answer 1

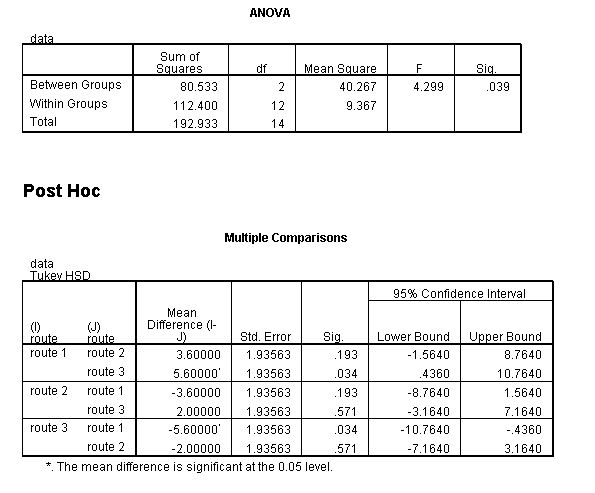
ANOVA
Source of Variation	DF	SS	MS	F VALUE	P VALUE
Section	2	80.533	40.267	4.299	0.039
Residuals	12	112.4	9.367

Population Mean Difference	diff	lwr	upr	p adj	Do the average times differ?
Route 2 - Route 1	-3.60	-8.764	1.564	0.193	NOT SIGNIFICANT
Route 3 - Route 1	-5.6	-10.764	-0.436	0.034	SIGNIFICANT
Route 3 - Route 2	-2.0	-7.1640	3.164	0.571	NOT SIGNIFICANT