Question

The processing time for the shipping of packages for a company, during the holidays, were recorded for 48 different orders. The mean of the 48 orders is 10.5 days and the standard deviation is 3.08 days. Raw data is given below. Use a 0.05 significance level to test the claim that the mean package processing time is less than 12.0 days. Is the company justified in stating that package processing is completed in under 12 days?

1) Write Ho (null) and H1 (alternative) and indicate which is being tested

2) Perform the statistical test and state your findings; Write answer as a statement

Days
4.4
8.8
8.2
11.5
11
15.3
10.3
10.9
4.8
13.6
8.1
4.1
12.5
9.9
11.3
13.1
13.6
7.6
10.3
11.7
8.9
4
9.5
8.1
16.3
13.7
12.4
8.6
13.8
7.1
6.9
11.3
9.9
11.8
12.2
11.4
6.2
10
12.7
11.3
13.2
12
9
10
13.3
16.8
14.9
7.7

Answer 1

Given data

population mean package processing time in days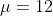

number of sample (n)=48

Sample mean package processing time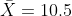

Sample standard deviation (S)=3.08

significance level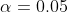

Now the claim is mean processing time is less than 12 days so the hypothesis will be

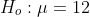
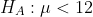
the test statistic will be

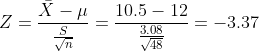
Since it is a lower tail test so from standard probability distribution table the Z critical value for 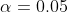is

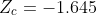
Since we can say that we have enough evidence to reject the null hypothesis

conclusion

as we have rejected the null hypothesis we can say that we have enough evidence to say that company justified in stating that package processing is completed in under 12 days.