Question

M&M candies have 6 different color coatings in a standard single serving bag: blue, brown, green, orange, red and yellow. However, the number of each color that occurs in an individual bag may not be proportional. If bags of M&M Milk Chocolate candies contained proportional counts by color, there should be about 17% green M&M’s. A sample of M&M Milk Chocolate bags consisted of 1093 M&Ms. There were 273 green M&M’s of the total M&M’s in the sample. Determine with an acceptable error rate of 1% if our M&M sample is consistent with the equal color proportion of 17% green M&M’s. H0: p = 0.17 The percentage of green M&M’s in bags of Milk Chocolate M&M’s is 17%. HA: p  0.17 The percentage of green M&M’s in bags of Milk Chocolate M&M’s is not 17%. 8. What is the sample proportion for green M&M’s? (2 points) 9. What would be the value of the appropriate test statistic for this hypothesis test? (5 points) 10. What is the P-value of the test statistic determined in question #9? (5 points) 11. What would be the decision for this hypothesis test? (i.e. reject or do not reject the null hypothesis?) (4 points) 12. State your conclusion, based on the selected decision in question #11, appropriate to the hypothesis test on percentage of green M&M’s in M&M bags. (5 points) 13. If we wish to have a margin of error of 0.05 or less, at least how many M&M’s should we have had in our sample? (Was our sample large enough?) (4 points)

Answer 1

Solution:-

8)

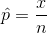
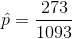
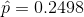
State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.

Null hypothesis: P = 0.17
Alternative hypothesis: P 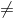0.17

Note that these hypotheses constitute a two-tailed test.

Formulate an analysis plan. For this analysis, the significance level is 0.01. The test method, shown in the next section, is a one-sample z-test.

Analyze sample data. Using sample data, we calculate the standard deviation (S.D) and compute the z-score test statistic (z).

S.D = sqrt[ P * ( 1 - P ) / n ]

S.D = 0.01136
z = (p - P) /S.D

z = 7.02

where P is the hypothesized value of population proportion in the null hypothesis, p is the sample proportion, and n is the sample size.

Since we have a two-tailed test, the P-value is the probability that the z-score is less than -7.02 or greater than 7.02.

Thus, the P-value = less than 0.0001.

Interpret results. Since the P-value (almost 0) is less than the significance level (0.01), we cannot reject the null hypothesis.

Reject the H₀.

13) The sample size required is 375.

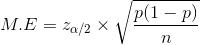
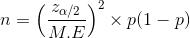
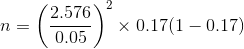
n = 374.52

n = 375