Question

Finding Z scores for a Standard Normal Distribution

1.) Find the z score that has an area of 0.4321 to its left

2.) Find the z score that has an area of 0.3675 to its right

Finding X scores for a Normal Distribution

3.) Find the x score that has an area of 0.8321 to its left. ( mean = 100, SD = 15)

4.) Find the x score that has an area of 0.78 to its right. ( mean = 200, SD = 20)

Answer 1

Z scores for a standard Normal distribution

1)

Z₁ be the z score that has an area of 0.4321 to it's left i.e P(Z 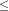Z₁) =0.4321

From Standard normal tables; P(Z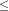-0.17) = 0.4325 (nearest to 0.4321)

Z₁ = -0.17

Z score = -0.17

z score that has an area of 0.4321 to its left = -0.17

2)

Z₂ be the z score that has an area of 0.4321 to it's right i.e P(Z <  Z₂) =0.3675

P(Z>Z₂) = 1-P(Z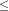Z₂) =1 - 0.3675=0.6325

From Standard normal tables; P(Z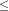0.34) = 0.6331 (nearest to 0.6325)

Z₂ = 0.34

Z score = 0.34

the z score that has an area of 0.3675 to its right = 0.34

X scores for a Normal Distribution

3.) x score that has an area of 0.8321 to its left  ( mean = 100, SD = 15)

X₁ : x score that has an area of 0.8321 to its left i.e P(X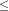X₁) = 0.8321

Z₁ be the z-score for X₁ : Z₁ = (X₁ - mean)/SD = (X₁-100)/15 ; X₁ = 100+15Z₁

P(Z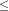Z₁) = P(X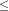X₁) = 0.8321

From standard normal tables,

P(Z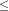0.96) = 0.8315(nearest to 0.8321)

Z₁ = 0.96

X₁ = 100+15Z₁ = 100 + 15 x 0.96 = 114.4

x score that ans area of 0.8321 to its left = 114.4

4.) x score that has an area of 0.78 to its right. ( mean = 200, SD = 20)

X₂: x score that has an area of 0.78 to it's right i.e P(X>X₂) = 0.78

Z₂ be the z-score for X₂ : Z₂ = (X₂- mean)/SD = (X₂-200)/20 ; X₂ = 200+20Z₂

P(X>X₂) = 1- P(X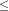X₂) = 0.78 ; P(X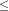X₂) =1-0.78=0.22

P(Z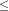Z₂) = P(X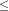X₂) = 0.22

From standard normal tables,

P(Z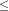-0.77) = 0.2206(nearest to 0.8321)

Z₂ = -0.77

X₂ = 200+20Z₂ =200 + 20 x -0.77 =200-15.4=184.6

x score that has an area of 0.78 to it's right = 184.6