Question

The population mean income of US residents is $50,000 with a standard deviation of $20,000. Suppose that we sample 300 US residents and calculate the sample mean.

a) What distribution does the sample mean follow? WHY? Write using proper notation.

b) Find the probability that the mean of our sample is less than $49,000

c) Suppose we sample 3,000 US residents instead. Find the probability that the mean of the sample is less than $49,000. Explain why this probability is smaller.

Answer 1

Here sample size is of 300 students

n = 300

population mean income = 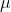= $ 50,000

standard deviation = 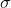= $ 20,000

(a) Here the distribution of sample mean follows normal distribution with expected mean is equal to $ 50,000 and standard error of 20000/sqrt(300) = $ 1154.70

(b) Here we have to find

P(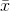 < $ 49000)

z= (49000 - 50000)/1154.70 = -0.866

so here

P(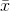 < $ 49000) = P(Z < -0.866) = 0.1932

(c) Here sample size = n = 3000

standard error = 20000/sqrt(3000) = $ 365.15

P(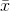 < $ 49000)

z = (49000 - 50000)/365.15 = -2.7386

P(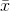 < $ 49000) = P(z < -2.7386) = 0.0031

so here the probability is smaller as population size is larger here so probability would be smaller.