Question

If p is any positive number between 0 and 1, then p4 + C(4,3) p3(1–p) + C(4,2) p2(1–p)2 + C(4,1) p (1–p)3 + (1–p)4 = 1. Explain why without performing any calculation.

Please explain the concept behind this to me, and not just the chain of calculations or mathematical proofs.

Answer 1

here p is a positive number between 0 and 1

let us look at the binomial distribution

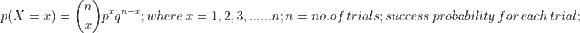
so p lies between 0 and 1

the right-hand side of the equation can be rewritten as

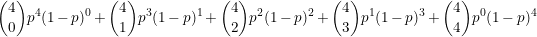
this is equivalent to the sum of n=4 terms of binomial distribution with parameters n,p

sum of n terms of a binomial distribution is equal to one since it is a probability distribution function

therefore

or elese we can do it another way

binomial expansion is given as

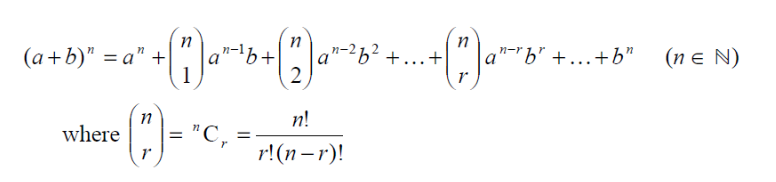
in our case n=4,a=p,b=1-p

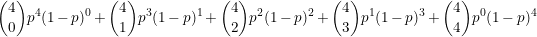
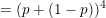
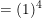
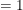
If we actually multiplied the (x + a)⁴,

then, before adding the like terms, we would find terms in

x⁴, x³a, x²a², xa³, and a⁴.

Multiplication of n binomials produces 2*2*2*2*2*......n times=2ⁿ terms.(distribution property)

For, multiplication of two binomials gives 4 terms:

(p + q)(m + n) = pm + pn + qm + qn.

If we multiply those with a binomial, we will have 8 terms; those multiplied with a binomial will produce 16 terms; and so on.

Example.   (x + a)(x + b)(x + c)(x + d)

=  x4	+ (a + b + c + d)x3 + (ab + ac + ad + bc + bd + cd)x2
	+ (abc + abd + acd + bcd)x + abcd.

For, each of the 2⁴ terms will consist of 4 factors: one from each binomial.

x⁴ is produced by taking x from each factor.

xxxx = x⁴.

There is only one such term.

The coefficient of x⁴ is 1.

Terms with x³

axxx + xbxx + xxcx + xxxd = (a + b + c + d)x³.

The coefficient of x³, therefore, is the sum of the combinations of a, b, c, d  taken 1 at a time

no.of such combinations ⁴C₁

terms with x²

(ab + ac + ad + bc + bd + cd)x².

The coefficient of x², therefore, is the sum of the combinations of a, b, c, d  taken 2 at a time

no.of such combinations ⁴C2

terms with x

(abc + abd + acd + bcd)x.

the coefficient of x, therefore, is the sum of the combinations of a, b, c, d  taken 3 at a time

There will be ⁴C₃ or 4 ways of doing that

terms with x⁰

abcd.

the coefficient of x⁰, therefore, is the sum of the combinations of a, b, c, d  taken 4 at a time

Finally, the constant term will be produced by taking the letter from each of the 4 factors. There is ⁴C₄ -- 1 -- way of doing that.
If a = b = c = d then we have the 4th power of (x + a ):

(x + a)4	=	4C0x4 + 4C1ax3 + 4C2a2x2 + 4C3a3x + 4C4a4
	=	x4 + 4ax3 + 6a2x2 + 4a3x + a4.

The result is general. The binomial theorem states that in the expansion of (x + a)ⁿ, the coefficients are the combinatorial numbers ⁿC_k , where k -- the exponent of a -- successively takes the values 0, 1, 2, . . . , n.

Each term in the expansion will have this form:

n       (n − k)k

an − kbk

.