Question

The quality control department of a factory has established that a lot containing 90% or more of good items in a lot of good quality. The following plan has been established. A sample of 4 items is taken if 1 or none is defective, the lot is accepted, otherwise a second sample of 2 items is taken if the second sample does not contain defective items, the lot is accepted, otherwise it is rejected. Assume that the lot is very large and therefore the probability of extracting a defective item is constant.

Calculate the probability of accepting a lot containing 25% of defective items.

Answer 1

Answer: The probability of accepting a lot containing 25% of defective items is 0.8855

Explanation:

For a lot containing 25% of defective items,

Probability of a piece being defective =0.25

For first sample:

n=4

Taking a sample of 4 can be considered as a binomial experiment with n=4 and success probability p=0.25.

Probability of no defective =

=1*0.25⁰*0.75⁴

=0.3164

Probability of one defective =

=4*0.25¹*0.75³

=0.4219

Probability of 2 or more defective

= 1-(0.3164+0.4219)

=0.2617

For second sample, we take sample of 2,

so n=2,

Probability of no defective =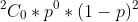

=1*0.25⁰*0.75²

=0.5625

Probability of accepting based on first sample =Probability of no defective + Probability of one defective

=0.3164+0.4219

=0.7383

Probability of accepting based on second sample

=Probability of 2 or more defects in first sample*Probability of no defect in 2nd sample

=0.2617*0.5625

=0.1472

Total probability of accepting lot = 0.7383 + 0.1472

=0.8855