Question

(b) Consider a 1D lattice with a two atom basis with N+1 atoms in total.

a. How many normal modes of vibration are there?

b. Draw a dispersion diagram to illustrate these modes.

c. Describe the motion of the atoms at three key points on the dispersion curve for a longitudinal vibration.

d. How can you interpret the principal quantum number, nk, for the k th vibrational mode?

e. In which branches and regions of the dispersion curve is an electromagnetic wave most likely to interact with the lattice vibration? Explain your answer.

Answer 1

Diatomic Basis - Identical Mass, Different Spacing:

(a) For a finite lattice of N+1 atoms we will obtain N+1 values of k that provide distinct solutions. We thus have 2(N+1) normal modes - unsurprising since there are 2(N+1) degrees of freedom. If we allow movement perpendicular to the line there are 4(N+1) transverse/longitudinal modes since each atom now has an additional degree of freedom perpendicular to the line.

(b) Plotting the solutions for w(k): Here we´ll consider that the interatomic forces change depending on the equilibrium spacing, which we account for by imagining springs of constants connecting the atoms. M₁ and M₂ are the masses of the atoms. (the plot is a general one and I have collected from internet. I am explaining the same below)

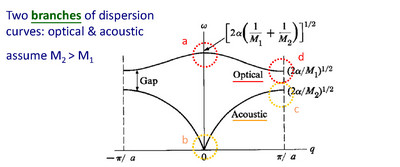
The two w vs. k curves shown are referred to as the branches of the dispersion relation. The lower curve is the reference curve for a 1D monatomic lattice, and is called the acoustic branch due to its small k behavior which is the characteristic of sound waves. The upper curve is called the optical branch, since these modes tend to interact with electromagnetic radiation.
Another notable feature is a gap in allowed frequency - a phononic gap.

(c) Acoustic Branch: In the case of the long-wave approximation (ak<<1) in acoustic branch the atoms move synchronously and deviation of every atom is about the same at any moment of the time. The heavy atoms in the cell oscillate out of phase with other heavy atoms, light atoms are at rest. The acoustic branch has this name because it gives rise to long wavelength vibrations which travel with the speed of sound. The 2 atoms generally vibrate with a small phase difference

Optical Branch: The optical branch describes all atoms within a primitive cell vibrating in phase against each other. Light atoms in the cell oscillate out of phase with other light atoms, heavy atoms are at rest. The optical branch is a higher energy vibration and they vibrate generally in out of phase. If the two vibrating atoms are ions, a dipole is created during the vibration that can interact with electromagnetic radiation giving optical properties to the crystal.

There are two possible modes of vibrations of atoms in the crystal: Longitudinal and transverse. In case of longitudinal mode the displacement of atoms from their equilibrium position coincides with the propagation direction of the wave or in opposite direction, whereas for transverse mode, atoms move perpendicular to the propagation of the wave.

Transverse Acoustic mode will be like this figure:

Transverse Optical mode will be like this figure: Amplitude of vibration is strongly exaggerated

(d) The dispersion relation is periodic in k with a period 2/a (a is the unit cell length). This result remains valid for a chain of containing an arbitrary number of atoms per unit cell. The energy of the lattice vibration is quantized. The quantum of energy is called a phonon in analogy with the photon in EM wave. The principal quantum number, nk, for the k th vibrational mode is the number of phonons.

(e) The optical branch is a higher energy vibration (the frequency is higher, and you need a certain amount of energy to excite this mode). The term “optical” comes from how these were discovered - notice that if atom 1 is +ve and atom 2 is -ve, that the charges are moving in opposite directions. You can excite these modes with electromagnetic radiation (ie. The oscillating electric fields generated by EM radiation)