Question

Think about a population mean that you may be interested in and propose a confidence interval problem for this parameter. Your data values should be approximately normal.

For example, you may want to estimate the population mean number of hours people watch tv each week. Your data could be that you spoke with seven people you know and found that they went out 14,20,17,26,2,12, and 16 times last week. You then would choose to calculate a 95% (or another level) confidence interval for the population mean.

Assume a random sample was chosen, which is required to determine a confidence interval.

please show all steps in the solution

Answer 1

From the data: , 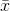= 15.286, s = 7.4098, n = 7

Since population standard deviation is unknown, the tcritical (2 tail) for 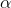= 0.05, for df = n -1 = 6, is 2.4469

The Confidence Interval is given by 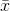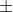ME, where

ME = tcritical * \frac{s}{\sqrt{n}} = 2.4469 * \frac{7.4098}{\sqrt{7}} = 6.853

The Lower Limit = 15.286 - 6.853 = 8.433

The Upper Limit = 15.286 + 6.853 = 22.139

The 95% Confidence Interval is (8.43 , 22.14)

__________________________________________________

Calculation for the mean and standard deviation:

Mean = Sum of observation / Total Observations

Standard deviation = SQRT(Variance)

Variance = Sum Of Squares (SS) / n - 1, where SS = SUM(X - Mean)².

#	X	Mean	(x - mean)2
1	14	15.286	1.65
2	20	15.286	22.22
3	17	15.286	2.94
4	26	15.286	114.79
5	2	15.286	176.52
6	12	15.286	10.80
7	16	15.286	0.51
			0.00
Total	107		329.4287

n	7
Sum	107
Average	15.286
SS	329.428572
Variance = SS/n-1	54.904762
Std Dev	7.4098