Question
In: Physics
Starting with Bernoulli’s equation, explain how to derive Bernoulli’s principle
Solutions
Expert Solution
Bernoulli’s principle can be derived from the principle of conservation of energy. This states that the total mechanical energy of the moving fluid comprising the gravitational potential energy of elevation, the energy associated with the fluid pressure and the kinetic energy of the fluid motion, remains constant.
Consider a fluid of negligible viscosity moving with laminar flow, as shown in Figure 1.
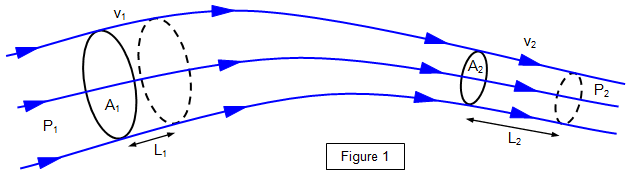
Let the velocity, pressure and area of the fluid column be
v1, P1 and A1 at Q and
v2, P2 and A2 at R. Let the volume
bounded by Q and R move to S and T where QS = L1, and RT
= L2. If the fluid is incompressible:
A1L1 = A2L2
The work done by the pressure difference per unit volume = gain in
k.e. per unit volume + gain in p.e. per unit volume. Now:
Work done = force x distance = p x volume
Net work done per unit volume = P1 - P2
k.e. per unit volume = ½ mv2 = ½ Vρ v2 =
½ρv2 (V = 1 for unit volume)
Therefore:
k.e. gained per unit volume = ½ ρ(v22 -
v12)
p.e. gained per unit volume = ρg(h2 –
h1)
where h1 and h2 are the heights of Q and R
above some reference level. Therefore:
P1 - P2 = ½ ρ(v12 –
v22) + ρg(h2 -
h1)
P1 + ½ ρv12 + ρgh1 =
P2 + ½ ρv22 +
rgh2
Therefore:
P + ½ ρv2 + ρgh is a constant
For a horizontal tube h1 = h2 and so we
have:
P + ½ ρv2 = a constant
This is Bernoulli's theorem You can see that if there is a increase
in velocity there must be a decrease of pressure and vice
versa.
No fluid is totally incompressible but in practice the general
qualitative assumptions still hold for real fluids.
Related Solutions
In applying bernoulli’s equation, derive an equation for the pressure at the inlet of the nozzle...
Bernoulli’s Principle This activity will allow you to see Bernoulli’s Principle in action. Some of the...
How is Bernoulli’s Principle equivalent to the Work Energy Theorem and the Conservation of Energy Principle?
Starting with the Keynesian cross, explain how to derive the IS curve
Research about one of this topic in 10 paper Buoyancy and Archimedes’ Principle Bernoulli’s Equation Simple...
Understand and be able to state the followings: • Archimedes’ Principle• Pascal’s Principle • Bernoulli’s Principle•...
Show how the terms of Bernoulli’s equation are related to Conservation of Energy?
Starting from the first and second law of thermodynamics, derive the fundamental equation for A in...
1. Starting from the enzyme-catalyzed reaction: S -> P Derive the (a) Michaelis-Menten Equation (b) starting...
5. (a) Write down the Bernoulli’s equation and the continuity equation. (b) The entry and exit...
- Many people have different concepts or ideas about the study of economics. It would be interesting...
- 2.70 moles of an ideal gas with CV,m=5R/2are transformed from an initial state T = 660....
- A 10 g bullet traveling at 430m/s str
- Suppose the Madison city government imposes a price ceiling on the rental price of apartments.The demand...
- Magnolia Manufacturing makes wing components for large aircraft. Kevin Choi is the production manager, responsible for...
- distinguish between microeconomics and macroeconomics
- Balloons By Sunset (BBS) is considering the purchase of two new hot air balloons so that...
 genius_generous answered 2 months ago
genius_generous answered 2 months ago