Question

In: Math

Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and...

Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows:

Department Product 1 Product 2 Product 3
A 1.70 3.20 2.20
B 2.40 1.40 2.90
C 0.45 0.45 0.45

During the next production period, the labor-hours available are 490 in department A, 390 in department B, and 90 in department C. The profit contributions per unit are $29 for product 1, $32 for product 2, and $34 for product 3. Use a software package LINGO.

  1. Formulate a linear programming model for maximizing total profit contribution. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300) If constant is “1”, it must be entered in the box.

    Let Pi = units of product i produced
    Max ______P1 + ______P2 + ______P3
    s.t.
    ______P1 + ______P2 + ______P3 ≤ ______
    ______P1 + ______P2 + ______P3 ≤ ______
    ______P1 + ______P2 + ______P3 ≤ ______
    P1, P2, P3 ≥ 0
  2. Solve the linear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution?

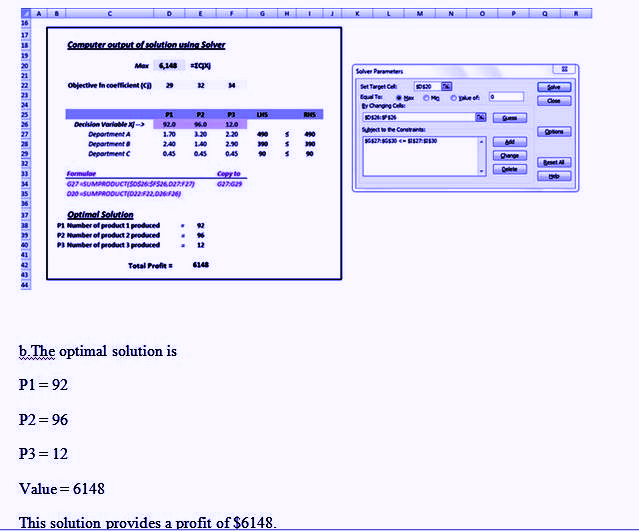
    P1 = ______
    P2 = ______
    P3 = ______

    Profit = $  ______
  3. After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had not been taken into account. She noted that setup costs are $440 for product 1, $590 for product 2, and $640 for product 3. If the solution developed in part (b) is to be used, what is the total profit contribution after taking into account the setup costs?

    Profit = $  ______
  4. Management realized that the optimal product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should not consider making more than 195 units of product 1, 170 units of product 2, or 160 units of product 3. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300) If constant is “1”, it must be entered in the box. Enter “0” if your answer is zero.

    Here introduce a 0-1 variable yi that is one if any quantity of product i is produced and zero otherwise.
    Max ______P1 + ______P2 + ______P3 + ______y1 + ______y2 + ______y3
    s.t.
    ______P1 + ______P2 + ______P3 ≤ ______
    ______P1 + ______P2 + ______P3 ≤ ______
    ______P1 + ______P2 + ______P3 ≤ ______
    ______P1 + ______y1 ≤ ______
    ______P2 + ______y2 ≤ ______
    ______P3 + ______y3 ≤ ______
    P1, P2, P3 ≥ 0; y1, y2, y3 = 0, 1
  5. Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the projected total profit contribution? Compare this profit contribution to that obtained in part (c). Enter “0” if your answer is zero.

    P1 = ______
    P2 = ______
    P3 = ______

    Profit = $  ______

    The profit is increased by $ ______.

Please fill out all the blanks! Thank you!!

Solutions

Expert Solution

milcah answered 3 hours ago
Next > < Previous

Related Solutions

Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows: Department Product 1 Product 2 Product 3 A 1.50 3.00 2.00 B 2.00 1.00 2.50 C 0.25 0.25 0.25 During the next production period the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $25 for product 1, $28 for product 2,...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows: Department Product 1 Product 2 Product 3 A 3.00 2.00 1.50 B 1.00 2.50 2.00 C 0.25 0.25 0.25 During the next production period the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $28 for product 1, $30 for product 2,...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows: Department Product 1 Product 2 Product 3 A 3.00 2.00 1.50 B 1.00 2.50 2.00 C 0.25 0.25 0.25 During the next production period the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $28 for product 1, $30 for product 2,...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and...
Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows: Department Product 1 Product 2 Product 3 A 2.00 1.50 3.00 B 2.50 2.00 1.00 C 0.25 0.25 0.25 During the next production period the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $30 for product 1, $25 for product 2,...
A company manufactures Products A, B, and C. Each product is processed in three departments: I,...
A company manufactures Products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for Departments I, II, and III are 900, 1080, and 840, respectively. The time requirements (in hours per unit) and profit per unit for each product are as follows. (For example, to make 1 unit of product A requires 2 hours of work from Dept. I, 3 hours of work from Dept. II, and 2...
A company manufactures Products A, B, and C. Each product is processed in three departments: I,...
A company manufactures Products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for Departments I, II, and III are 900, 1080, and 840, respectively. The time requirements (in hours per unit) and profit per unit for each product are as follows. (For example, to make 1 unit of product A requires 2 hours of work from Dept. I, 3 hours of work from Dept. II, and 2...
A company manufactures Products A, B, and C. Each product is processed in three departments: I,...
A company manufactures Products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for Departments I, II, and III are 900, 1080, and 840, respectively. The time requirements (in hours per unit) and profit per unit for each product are as follows. (For example, to make 1 unit of product A requires 2 hours of work from Dept. I, 3 hours of work from Dept. II, and 2...
ABC products makes parts for car engines. three departments (A, B and C) are involved in...
ABC products makes parts for car engines. three departments (A, B and C) are involved in the manufacturing process. The budgets for departmental overhead costs are $25,000, $45,000 and $30,000 respectively, which are allocated to products based on direct labor hours. Estimates of direct labor hours for each department are 5,000 7,000 and 10,000 hours respectively. The business-wide overhead absorption rate is: a. $3.00 b. $4.55 c. $4.81 d. 5.00
A manufacturing company makes three products, A, B, and C. The fixed FO is $60,000, consisting...
A manufacturing company makes three products, A, B, and C. The fixed FO is $60,000, consisting of $10,000 for material handling, material waste, and procurement; $30,000 for rent and utilities; and $20,000 for safety and canteen costs. Other costs are shown in Table 6.16 Product A Product B Product C Number of Units Produced Per Month (-)       250 400 900 Total Material Costs Per Month ($)     5000 8000 4000 Labor Hours Per Unit (hr) 4 3.5 1.5 Labor Rate Per...
Sonata Corporation makes three types of products—Model Z, Model EF, and Model DS. The manufacturing operations...
Sonata Corporation makes three types of products—Model Z, Model EF, and Model DS. The manufacturing operations are mechanized and there is no direct labor. Manufacturing overhead costs are significant, and Destiny has adopted an activity-based costing system. Direct materials costs per unit for each model are as follows: Model Z           $93 Model EF         $88 Model DS        $127 Sonata Corporation has 5 activities—assembly, materials management, testing, inspecting and milling. The cost driver for assembly is machine hours. Total costs and production...
ADVERTISEMENT
Subjects
ADVERTISEMENT
Latest Questions
ADVERTISEMENT