Question

1.

Suppose a firm pays labor (L) a wage rate (w) of $10 and capital (K) a rental rate (r) of $25.

A.

Write an equation for the isocost line and find i

ts slope. Then, draw a graph (with Labor on

the horizontal axis) of the isocost lines for Total Costs of $200 and $300.

B.

Suppose a firm wants to produce 200 units and can do so with the following combinations of

labor and capital

:

(5 L, 10 K); (10 L, 4 K

)

;

or (25 L, 2 K).

Using this information, o

n the same

graph as Part (A), draw

an approximate

isoquant for 200 units, making sure to show the

cost

-

minimizing output choice.

Answer 1

A)

Given

Wage rate=w=$10

Capital Rent=r=$25

Isocost line is given by

C=wL+rK

C=10L+25*K (Equation of isocost line)

On rearranging we get

25K=C-10L

K=0.04C-0.4L

Comparing with general equation of line i.e. y=mx+c, we can say that slope of isocost line is -0.40.

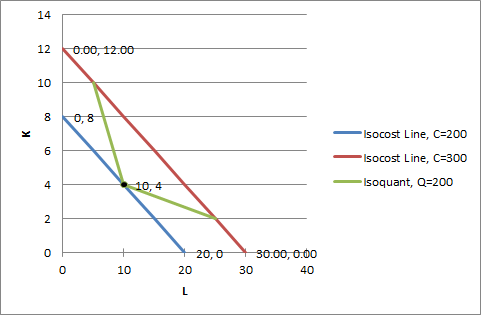
Let us draw isocost lines for C=200 and 300

In case of C=200, We can develop the following schedule

L	K=0.04*200-0.4*L
0	8
5	6
10	4
15	2
20	0

In case of C=300, We can develop the following schedule

L	K=0.04*300-0.4*L
0.00	12.00
5.00	10.00
10.00	8.00
15.00	6.00
20.00	4.00
25.00	2.00
30.00	0.00

b)

For Q=200, We can use the given schedule to draw isoquant curve

L	K
5	10
10	4
25	2

We can see that isocost line (C=200) is tangent to isoquant line (Q=200) at L=10 and K=4

It represents the cost minimizing input combination.

Minimum Cost is $200